問題
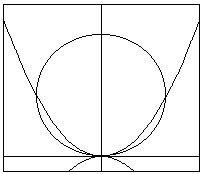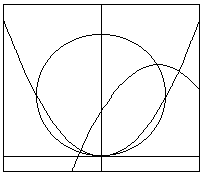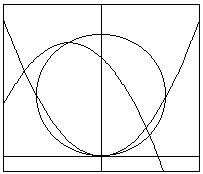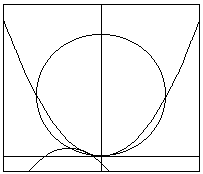
点(0.1)を中心とし、半径が1の円をC、放物線y=x2をC1とする。
また、円C上に頂点Aを持つ放物線y=-(x-p)2+qをC2とする。
(1)C2の頂点Aが原点以外にある時、C1とC2は異なる2点で交わることを示し、その交点のx座標を求めよ。
(2)C1とC2によって囲まれる図形の面積をSとする。C2の頂点Aが円C上を動くとき、Sの最大値とそのときのAの座標を求めよ。
解答
(1)
C1 と C2 を連立させて、
x2=-(x-p)2+q …(i)
展開して整理すると、
2x2-2px+p2-q=0
判別式をとって、
D/4=p2-2(p2-q)=-p2+2q
(p, q) は C2 の頂点であり、円 C 上にあるので、
p2+(q-1)2=1
p2=1-(q-1)2
判別式に代入して、
D/4=(q-1)2-1+2q=q2
よって、q≠0 のとき、D>0 なので、(i) は異なる2実解を持ち、
C1, C2 は異なる2点で交わる。
また、(i) を解くと、
x=(p±√(D/4))/2=(p±√q2)/2
q は 円C 上の原点を除く点のy座標なので、q>0 より、
x=(p±q)/2
(2)
f(x)=x2
g(x)=-(x-p)2+q
とすると、求める面積Sは、g(x)-f(x) を (p-q)/2 から (p+q)/2 まで積分した値である。
一方、α=(p-q)/2、β=(p+q)/2 とすると、α、βは 、g(x)-f(x)=0 の解なので、
g(x)-f(x)=-2x2+2px-p2+q=-2(x-α)(x-β) と書け、Sは
S=-2(α-β)3/6=q3/3
0<q≦2 より、q=2 のとき、Sは最大で、最大値は8/3。このときAは(0, 2)。
算数・数学の部屋に戻る