問題
半径1の円を底面とすろ直円柱2本が、直角に交差している。2つの円柱の重なった部分の立体について、
(1)体積を求めよ。(横に輪切りにしてカバリニリの原理を使う、半径1の球の体積との比)
(2)葉っぱのような図形を4枚つなげれば、この立体をつくることが出来る。この葉っぱの形を調べよ。(曲線を関数の式として表せ)
解答
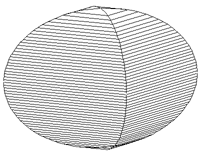
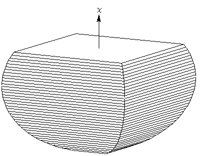
(1)重なった部分の立体は、上図のような立体で、右図のように、x軸をとり
x軸に垂直な面でこの立体を切ると、正方形になります。
一方、半径1の球をこの立体に重ねて同じように切ると、断面は、上述の正方形に
内接する円になります。
任意の断面について同じことがいえるので、上図の立体の体積は、
(半径1の球の体積)×(正方形の面積)÷(円の面積) なので、
4π/3×4÷π=16/3
(2)上図の断面の正方形の幅を2wとします。
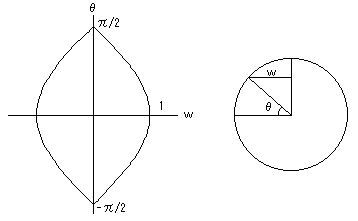
右図のθの位置でのwの値は、cosθに当たります。
-π/2〜π/2 の範囲において、
w=±cosθ
となります。
「算数・数学」の部屋に戻る