月の光さんからの質問１

問題

今日数学のテストで一問分らない問題があったので教えてください。
　　ただし（０＜ａ＜ｂ）
の表面積を求めよ。グラフも書いていただけるとうれしいです。

解答
　
とおくと、予式は
　・・・(1)
となり、ｒ−ｚ平面上で、(b,0) 中心、半径ａの円になります。

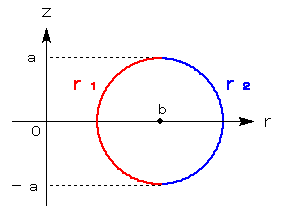
求める立体は、この円をｚ軸を中心に回転させたものになります。
(1) をｒについて解くと、
　
となります。ここで、
　，
とおくと、図の円のｚ軸に近い方の半分がｒ_１，ｚ軸から遠い方の半分がｒ_２となります。

求める表面積Ｓは、

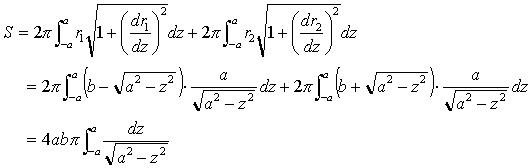
ｚ＝ａｓｉｎθとおくと、−ａ＜ｚ＜ａ は、π/２＜θ＜π/２ に対応し、ｄｚ＝ａｃｏｓθｄθ。
この範囲では、ｃｏｓθ＞０ なので、


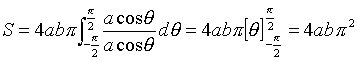
となります。　　　　　　　　　　　　　　　　　　　　　　答え　４ａｂπ²

パップス・ギュルダンの定理(Pappus-Guldinus theorem)というそうです。
　（表面積）＝２π×（回転軸から図形の周の重心までの距離）×（図形の周長）

ちなみに体積は、
　（体積）＝２π×（回転軸から図形の重心までの距離）×（図形の面積）

算数・数学の部屋に戻る