問題
球を任意の平面で切り取ったとき,切り取った球の一部の重心の求め方を教えてください。
解答
ここでは、半球(ちょうど2等分したときの片方)か、それより小さい方の立体について考えます。
残りの立体も、同様に考えるか、大小あわせて、体積で比例配分して、全球の重心が中心にくるように
大きい立体の重心位置を決めればできます。
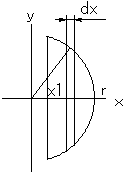
球の半径をrとし、切り口の平面が、中心から x1 の距離にあるとします。
ただし、0≦x1<r。
切り口に垂直な方向にx軸を取ります。
中心から x(x1≦x<r) の位置に、厚さdx(微小量)の円盤を考えます。
この円盤の半径をyとすると、y=√(r2−x2) より、円盤の底面積は
S=πy2=π(r2−x2)
S・dxを、x1からrまで積分すると、体積が出ます。
V=π∫(x1〜r)(r2−x2)dx=π[r2x−x3/3](x1〜r)=π(2r3/3−r2x1+x13/3)
一方、球の密度を1とし、各円盤の原点まわりのモーメント xSdx を
x1からrまで積分すると、原点まわりのモーメントが出ます。
I=π∫(x1〜r)(r2x−x3)dx=π(r4/4−r2x12/2+x14/4)
よって、重心の原点からの位置は、
I/V=(r4/4−r2x12/2+x14/4)/(2r3/3−r2x1+x13/3)
となります。
参考までに、半球(x1=0 の場合)は、重心の位置は
原点から3r/8 の位置。
算数・数学の部屋に戻る