問題
関数f(x)＝ｘ3＋ax2＋（b-a-1)xについて次の問に答えよ。
（１）f(x)がｘ≧０で単調増加するような点（a，ｂ）の範囲Gを図示せよ。
（２）ｘ≧０におけるｙ＝f(x)の逆関数をｘ＝f-1（ｙ） （ｘ≧０）とする。点（a，ｂ）がGを動くとき
定積分
の最小値を求めよ。解答
（１）f(x) を x で微分して、
f'(x)＝３ｘ2＋２ａｘ＋（ｂ−ａ−１）
これが、ｘ≧０で常に正になるためには、y=f'(x) のグラフが、以下のようになるとき。
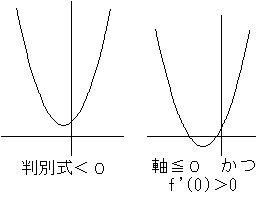
i) 判別式＜０
判別式をＤとすると、
Ｄ/4＝ａ2−３（ｂ−ａ−１）＜０
より、
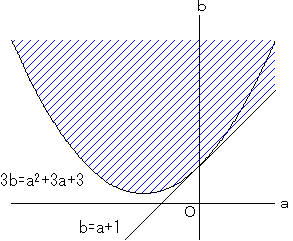
３ｂ＞ａ2＋３ａ＋３
３ｂ＞(ａ＋３/２)2＋３/４
ｂ＞(ａ＋３/２)2/３＋１/４ ………(a)
ii) 軸≦０ かつ f'(0)＞０
軸の式は ｘ＝−ａ／３≦０
より、 ａ≧０ ………(b)
f'(0)＝ｂ−ａ−１＞０
より、ｂ＞ａ＋１ ………(c)
以上より、（ａ，ｂ）の範囲は以下の通り。
ただし、境界線上の点は含まない。
（２）
は、下図の斜線部分の面積を表す。
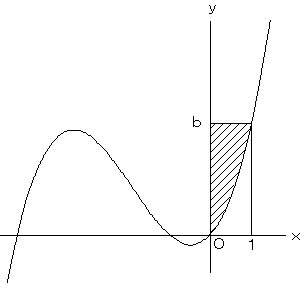
ｘ3＋ax2＋（b-a-1)x＝ｂ となるのは、ｘ＞０ではｘ＝１であるので、
求める定積分は、
となる。（１×ｂの長方形から斜線部以外を引く）＝ｂ−{1/4+a/3+(b-a-1)/2}＝b/2+a/6+1/4
k=b/2+a/6+1/4
３ｂ＝−ａ＋６ｋ−３/２
（１）の答えのグラフに ３ｂ＝−ａ＋６ｋ−３/２ のグラフを重ねて、
（１）の領域と共有点を持ちつつ、ｙ切片をできるだけ小さくした時が、
ｋの最小値となる。
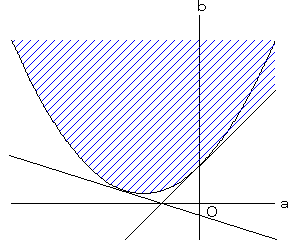
３ｂ＝ａ2＋３ａ＋３ と ３ｂ＝−ａ＋６ｋ−３/２＝−ａ＋Ｍ を連立させて、判別式＝０ とすると、
Ｍ＝−１ （ａ＝−２，ｂ＝1/3 のとき）
６ｋ−３/２＝−１ より、
ｋ＝1/12
算数・数学の部屋に戻る