橋本さんからの質問１

体積（容量）計算をお教えください。
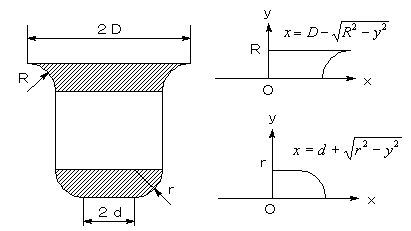
理科の実験で使用するビーカーを想像してください。
開口部にも底の部分にもＲ部分があります。
それぞれのＲ（半径）をｒ１、ｒ２ とし、高さｈ、直径ｄの場合の体積を出す方程式をお教えください。

解答

寸法を表す記号および、その位置は変えてあります。

円柱状の部分の体積はすぐ出ます。
また、底の部分と口の部分の体積の出し方は、同じですので、底の部分のみ求めます。

ビーカーの断面図に座標軸を設定し、ビーカー面の切り口の曲線の式を作ると、
上図右のようになります。

求める体積をＶとすると、Ｖは以下の式で求められます。

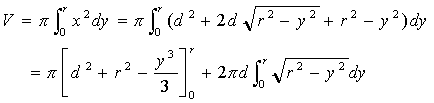
第２項の積分は、ｙ＝ｒsinθ と置いて、置換積分します。
　ｙ＝ｒsinθ
と置くと、０≦ｙ≦ｒ は ０≦θ≦π/２ に相当し、この範囲では、
　√(ｒ²−ｙ²)＝ｒcosθ
また、ｄｙ＝ｒcosθｄθ　より、
　
一方、
　２cos²θ＝cos2θ＋1
より、求める体積Ｖは、



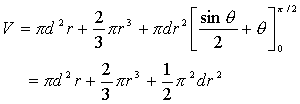
算数・数学の部屋に戻る