問題
xy平面上において、放物線C:y=−x2/a2+(a+6)x/3a (a>0)
と、x軸とで囲まれる部分をD1とし、4点O(0,0),A(4,0),B(4,4),C(0,4)を頂点とする正方形の内部と周をD2とする。
(1)放物線Cはaの値によらず直線 y=[ア]x/[イ] + [ウ]に接する。
(2)D1⊆D2となるようなaの範囲は、0<a≦√[エオ] − [カ] である。
(3)D1∩D2の面積S(a)はa=[キ]/[ク]のとき、最大値[ケコ]/[サ]をとる。
解答
(1)
y軸に平行な直線に接することはあり得ないので、求める直線を
y=mx+n
とおきます。y=−x2/a2+(a+6)x/3a と連立させて、
x2/a2−(a+6)x/3a+mx+n=0
x2/a2−{(a+6)/3a+m}x+n=0
判別式を取って、
D={(a+6)/3a+m}2−4n/a2
={(9m2+6m+1)a2+(36m+12)a+(36−36n)}/9a2
これがaに関係なく0になるためには、
9m2+6m+1=0
36m+12=0
36−36n=0
よって、m=-1/3、n=1
求める式は、 y=−x/3+1 ・・・答(1)
(2)
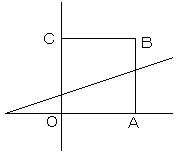
この放物線の軸は、
x=(a2+6a)/6>0 (aに対して単調増加)
であり、
y=−x2/a2+(a+6)x/3a
のグラフは、原点を通ることから、x軸とのもう一つの交点が点Aであるときが、
aの最大である可能性があります。またそのようなとき、もし、頂点が正方形OABCの外部にあるなら、
(1) で求めた直線を突き抜けてしまうので、点Aを通るときのaが(存在するなら)最大になります。
y=−x2/a2+(a+6)x/3a
に、x=4,y=0 を代入して、
−16/a2+4(a+6)/3a=0
これを解いて、
a=−3±√21
a>0 より、 a=√21−3 ・・・答(2)
(3)
aが変化すると、放物線は、図のように変化します。
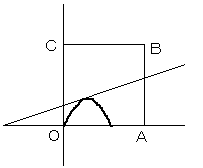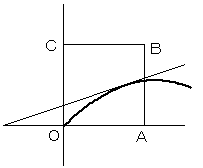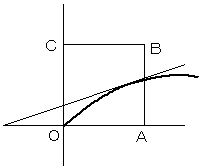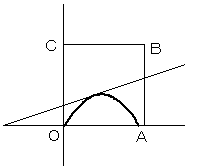
a<√21−3 のときより、a≧√21−3 (D1 がD2からはみ出している)の方が、面積は大きくなります。
その面積は、−x2/a2+(a+6)x/3a を、x=0から4まで積分すれば求められます。
∫0〜4(−x2/a2+(a+6)x/3a)dx=[−x3/3a2 + (a+6)x2/6a]0〜4
=8(a2+6a−8)/3a2
aで微分して、-144a2+384a/9a4
これが0になるのは a=0、8/3
よって、a>0 の範囲では、a=8/3 が極大(かつ最大) になります。
このとき、面積は、
8(a2+6a−8)/3a2=17/3 答 a=8/3 のとき 最大値 17/3
算数・数学の部屋に戻る