tを媒介変数として表せるサイクロイドの一部
C:x=t-sint, y=1-cost (0≦t≦2π)がある。
傾き-1/√3の直線Lが曲線Cと点Pで接している。
(1)接線Pの座標と直線Lの方程式を求めよ。
(2)曲線と直線およびX軸の x≧2π の部分とで囲まれた図形の面積Sを求めよ。
解答
(1)
媒介変数表示された式の微分係数の公式
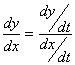
を用いて、 dy/dx= -1/√3 となる点を見つける。
dy/dt = sint
dx/dt = 1-cost
より、
√3・sin t = -1 + cos t
√3・sin t - cos t= -1
sin t・cos π/6 - cos t・sin π/6 = -1/2
三角関数の加法定理より、
sin(t-π/6) = -1/2
これを、0≦t≦2π で解くと、
t=4π/3 または 2π
ただし、t=2π は、分母=0 となり不適。
よって、t=4π/3 となり、点Pの座標は、
(x,y)=(4π/3+√3/2,3/2)
Lの方程式は、
y−3/2=-1/√3・(x−4π/3−√3/2)
整理して
y=−√3x/3+4√3π/9+2
(2)
Lの方程式で y=0 とおき、x軸との交点を調べると、
x=4π/3+2√3
よって、面積を求める図形は、以下のようになる。
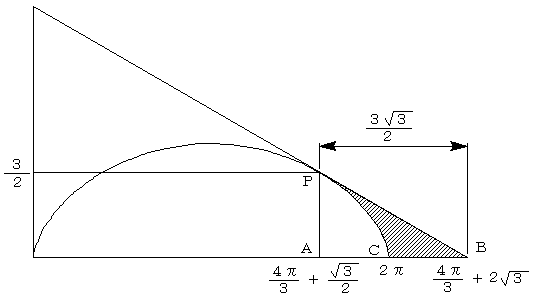
つまり、△ABPの面積から、サイクロイドを含む図形ACP(以下図形Mと呼ぶ)の面積を
引けばよい。
△ABPの面積は
1/2 × 3/2 × 3√3/2 = 9√3/8
図形Mの面積は
サイクロイドの式を、y=f(x) とおくと、
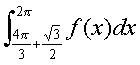
で求められます。これを、媒介変数tを用いると、
y=1 - cos t
dx = (1 - cos t)dt
より、上式は、
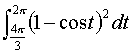
と書ける。
(1 - cos t)2 = 1 - 2cos t + cos2t
= 1 - 2cos t + (1 + cos 2t)/2
= 3/2 - 2cos t + cos 2t/2
より、上式を計算して、
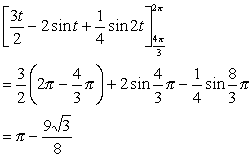
よって、求める面積は、
9√3/8 - (π - 9√3/8) = 9√3/4 - π
「算数・数学」の部屋に戻る