まりさんからの質問1
部分積分の公式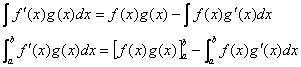 |
問題1
曲線 y=x+2sinx と x軸 、および直線 x=2π で囲まれた部分の面積を求めよ。
また、その部分を x軸のまわりに回転してできる回転体の体積を求めよ。
解答1
y’=1+2cosx
より、y’=0 となるのは x=2π/3、4π/3 および、それに2πの整数倍を加えた数。
よって、0≦x≦2π の範囲での増減表は
| x | 0 | 2π/3 | 4π/3 | 2π | |||
| y’ | + | + | 0 | − | 0 | + | + |
| y | 0 | 増 | 2π/3+√3 | 減 | 4π/3−√3 | 増 | 2π |
となり、4π/3−√3>0 より、y=x+2sinx のグラフはこの範囲で常にy≧0です。
(x軸と 原点以外で交わらない→面積を求めるのに積分するだけで良い)
さらに、f(x)=x+2sinx とすると、f(x+2π)=f(x)+2π なので、xが2πより大きい部分で
x軸と交わることもない。
また、f(-x)=-f(x) より、このグラフは原点について対称であるので、x<0の範囲でも、
x軸と交わることはない。
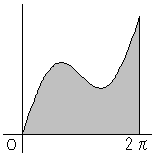
以上より、求める面積Sは、
S=∫0〜2π(x+2sinx)dx=[x2/2−2cosx]0〜2π=2π2
回転体の体積Vは、
V=π∫0〜2πy2dx=π∫0〜2π(x+2sinx)2dx
=π∫0〜2π(x2+4xsinx+4sin2x)dx
∫0〜2πx2dx=[x3/3]0〜2π=8π3/3
∫0〜2π4xsinxdx=-4∫0〜2πx(cosx)’dx=-4[xcosx]0〜2π+4∫0〜2πcosxdx
=-4[xcosx]0〜2π+4[sinx]0〜2π=-8π
∫0〜2π4sin2xdx=∫0〜2π2(1−cos2x)dx=[2x−sin2x]0〜2π=4π
よって、
V=π(8π3/3−4π)=8π4/3−4π2
問題2
自然数nに対し、In=∫1〜e(logx)n dxとおく。
部分積分法を使ってIn=e−nIn-1を示せ。またI1, I2, I3, I4 を求めよ。
解答2
上の公式において、f(x)=x、g(x)=(logx)n とおく。
In=∫1〜e(logx)ndx=∫1〜ex’(logx)ndx
=[x(logx)n]1〜e−∫1〜ex{(logx)n}’dx
一方
{(logx)n}’=n(logx)n-1×(logx)’=n(logx)n-1/x
より、
In=[x(logx)n]1〜e−∫1〜en(logx)n-1dx
=e−n∫1〜e(logx)n-1dx
=e−nIn-1 ・・・ 答1
I1=∫1〜elogxdx=∫1〜ex’logxdx=[xlogx]1〜e−∫1〜ex・(1/x)dx
=[xlogx]1〜e−[x]1〜e=1
I2=e−2I1=e−2
I3=e−3I2=e−3(e−2)=−2e+6
I4=e−4I3=e−4(−2e+6)=9e−24
算数・数学の部屋に戻る