並べて4桁の整数をつくる。2の倍数は何個あるか。
(2)男子10人、女子5人の中から合計3人の代表者を選ぶ方法は何通りあるか。
また、代表者3人のうちに女子が少なくとも1人含まれるような選び方は何通りあるか。
A君、B君のどちらか1人だけが選ばれるのは何通りあるか。
または4等分した直線で囲まれる長方形は、全部で何個あるか。
(1) 正三角形ができる確率 (2) 正三角形ができない確率
(3) 正六角形と辺を共有する三角形ができる確率
規則:硬貨を1枚投げて、表が出たらx軸の正の向きに1、裏が出たらy軸の正の向き に1だけ動かす。
硬貨を4回投げ終わったとき、移動後の点Pの座標が次のようになる確率を求めよ。 (1) (1,3) (2) (4,0)
(1)出る目の和の期待値 (2)出る目の差の期待値
この中から8個の果物を選ぶ。ただし、同種の果物については区別がないものとする。つぎのア〜コを求めよ。
(1)どの果物も少なくとも2個は選ぶとき、そのような選び方は全部でア通りある
また8個の果物を選ぶ選び方は全部でイウ通りある。このうち、同種のくだものを6個以上含まない選び方は全部でエオ通りあ る。
(2)ミカン4個、リンゴ2個、ナシ2個を選んだとき、選んだ8個を1列に並べる並べ方は全部でカキク通りある。
またこの8個を円形に並べるとき、その並べ方は全部でケコ通りある。
(1)最初の持ち点は2点である。
(2)さいころを投げて、奇数の目がでれば持ち点が1点増し、偶数の目が出れば持ち点が1点減る。
このような操作を5回行う。ただし途中で持ち点が0になったら、その時点でゲームは終了する。 このゲームについて5回のさいころを投げることができる確率、および、ゲームが終わった時の持ち点の期待値をもとめよ。
このうち3個は赤球で、残りの(n−3)個は白球である。
この袋から1個ずつ球を取り出す試行を考える。ただし、取り戻した球は元へ戻さない。
赤球を3個取り出したら、そこで試行は終わるものとする。
試行が終わるまでに取り出した球の総数を表す確率変数をXとし、X=kとなる確率をPkとする。
このときのP3、P4、PkとXの期待値を求めなさい。
A,B2人がAから始めて交互に箱の中から1球を取り出し、先に白玉を取り出したものを勝ちとする。
A,Bそれぞれの勝つ確率を求めなさい。
ただし、取り出した球は、箱にもどさないものとする。
(1) 1または6の目が3回だけでる確率
(2) 1または6の目が3回だけ連続して出る確率
をそれぞれ求めよ。
(1) 1回の得点の期待値はいくらか?
(2) 3回の得点の合計が5になる確率はいくらか。
4組の夫婦、合計8名の男女が1つの円卓で会食するために、
その座席を抽選によって決める。どの夫婦も隣り合った席に座る確率を求めよ。
問題2
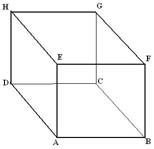
図のような立方体ABCD−EFGHにおいて、辺上を動くPがある。
Pが頂点Aを出発し他の頂点を全て一度だけ通りAに戻る方法は何通りあるか?
2人が勝ち2人が負ける、3人が勝ち1人が負ける、だれも勝たない(あいこにな
る)の4通りの場合がある。
(1)グー、チョキ、パーの出し方は全部で何通りあるか。 答:81
またそのうちだれも勝たない場合は何通りか。 答:39
(2)Aだけが勝つ確立は何か。 答:27分の1
4人のうち2人が勝つ確立は何か。 答:9分の2
(3)勝った人で300点を平等に分けるとき、つまり、1人だけ勝ったときは300点、
2人→150点、3人→100点ずつに分けるとき、Aの得点の期待値は何点か。 答:
9分の350点
2.周の長さが6の円周上に6個の点A,B,C,D、E,Fが等間隔に並んでいる。動点Pは、
さいころを1回投げて、3の倍数の目が出ると反時計回りに2だけ進み、それ以外の
目が出ると時計回りに1だけ進むものとする。(Pは、はじめに点Aにいる)
(1)さいころを2回投げた時、点PがEに到達する確立は? 答:5/9
(2)3回投げた時、PがAに到達する確立は? 答:13/27
(3)4回投げた時、Pが到達する点は何個あるか。 答:2
そのうちFに到達する確立は? 答:40/81
Cに到達する確立は? 答:41/81
(4)5回投げた時、PがDにとまらず通過してBに到達する確立は?
答:4/243
3.7行7列のマス目がある。最初に1行4列のマス目にいた人が、次の規則に従って
マス目を移動する。
<規則>
硬貨を同時に2枚投げて、
・表が2枚の時左に1上に2移動
・表1枚、裏1枚の時上に1移動
・裏2枚の時右に1上に2移動
(1)1回硬貨を投げて3行目にいる確立は? 答:1/2
2回投げて5列目にいる確立は? 答:1/4
(2)3回投げて、偶数番目の行にいる確立は? 答:1/2
7行3列にいる確立は? 答:3/64
(3)3回投げて、たどり着いた行の番号がその人の得点になるとき、その得点の期
待値は? 答:11/2点
4.4個のさいころを同時に投げる。
(1)4つの目がすべて異なる確率は? 答:5/18
(2)4つの目の積が偶数となる確率は? 答:15/16
(3)4つの目の和が6以下になる確率は? 答:15/6の4乗
(4)4つの目のうち最大のものが5である確立は? 答:41/144
玉には中心に穴が開いているとする。これらの玉に糸を通して指輪を作る方法は何通りあるか?
それらに記入されている数のうちから大きい方をA君の得点とする。
B君は、さいころを2回投げて2つの出る目の数の小さくない方をB君の得点とする。
A、B両君のうち得点の高い方を勝ちとする。
A君の勝つ確率とB君の勝つ確率の大小を比較せよ。
つぼの中に6個の赤球と4個の白球が入っている。
引き続き2球を取り出すとき、第1球が白で第2球が赤である確率を求めてください。
問題2
1からnまでの数字を書いたn枚のカードが箱に入っている。
箱の中から非復元抽出によって2枚のカードを取り出す。
A=最初に数字iのカードが現れる。
B=2番目に数字jのカードが現れる。
このとき次の確率を求めてください。
(1)P(B|A)
(2)P(A∩B)
問題3
大小2個のサイコロを投げて出る目を読む。
A=目の数の和は8
B=大のサイコロの目の数は4
とおきます。 このときP(B|A)を求めてください。
問題4
ある計算機センターにはH社、N社、F社の3社の端末が設置されている。
その割合はそれぞれ20%、30%、50%である。
また、各社の製品の不良品をうむ確率はそれぞれ0.5%、0.2%、0.1%である。
(1)任意に端末1台を取り出すとき、それらが不良品である確率は?
(2)取り出した端末が不良品とわかったとき、それがH社のものである確率は?
問題5
ある入学試験において受験生100人中80人は塾に行っており、20人は行っていなかった。
そして塾経験者の6割は合格し、行っていなかったものの3割が合格した。
任意の合格者が塾に行っていた確率はいくつでしょうか?
1回目に出る数をx、2回目に出る数をyとして、
座標平面上の点(x,y)を決める。
この試行を独立に2回繰り返して決まる2点と点(0,0)とで
決まる図形(三角形または線分)について
(1)図形が線分になる確率を求めよ。
(2)図形の面積の期待値を求めよ。但し、線分の面積は0とする。
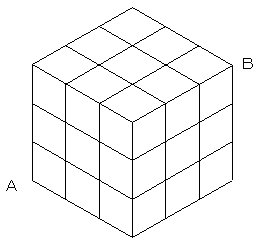
図のように、立方体の各面を9等分するような格子状の線が引かれている。
この格子線(立方体の辺を含む)を通り、AからBまで行くとき、最短距離で行く行き方は何通りあるか。