問題
次のようなゲームがある
(1)最初の持ち点は2点である。
(2)さいころを投げて、奇数の目がでれば持ち点が1点増し、偶数の目が出れば持ち点が1点減る。
このような操作を5回行う。ただし途中で持ち点が0になったら、その時点でゲームは終了する。
このゲームについて5回のさいころを投げることができる確率、および、ゲームが終わった時の持ち点の期待値をもとめよ。
解答
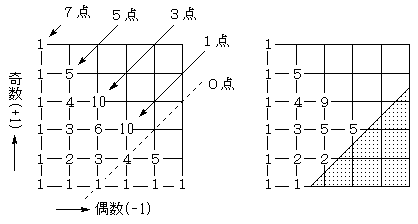
図のような碁盤目の左下をスタートとし、偶数が出れば、右に1つ、
奇数が出れば上にひとつ進むものとします。
スタートから、各地点まで行く進み方は、数字の通りです。
(左の数と下の数の和が、その位置の数になります)
また各位置での点数は、左図のように、斜めに同じ点数が並びます)