問題
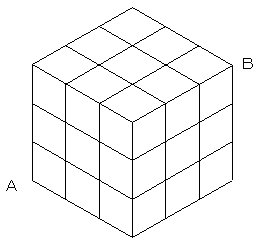
図のように、立方体の各面を9等分するような格子状の線が引かれている。
この格子線(立方体の辺を含む)を通り、AからBまで行くとき、最短距離で行く
行き方は何通りあるか。
解答1
かかさんからの質問1
問題

図のように、立方体の各面を9等分するような格子状の線が引かれている。
この格子線(立方体の辺を含む)を通り、AからBまで行くとき、最短距離で行く
行き方は何通りあるか。
解答1

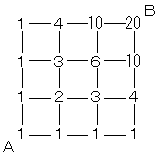
平面の場合、上図のように、AからBに行く方法を見つけるとき、
格子点上に左からと下から来る数字を足して記入すれば、行き方は
20通りと求められます。
立体の場合も同様に
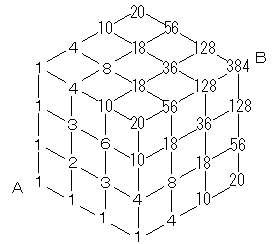
384通り と求められます。
解答2
格子点と格子点の間を1歩と言うとすると、
AからBまでは9歩で行くのが最短です。
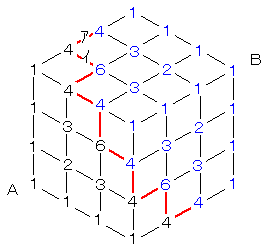
図は、Aから4歩目と5歩目の道を赤く示したものです。
黒い数字は、Aから赤い道の手前まで行くときの行き方、
青い数字は、Bから赤い道の手前まで行くときの行き方です。
例えば、アの道を通る方法は、4×4=16通り、イの道を通る方法は
4×6=24通りあります。
これらをすべて足すと、
16×6+24×12=384(通り)
解答3
AからBに最短で行く道は、必ず下図のような、3×6の長方形(元の立方体の面2枚)内に収まります。

この図で、AからBに行く方法は84通り。
面2枚を選ぶのは図のように6通り。
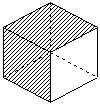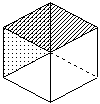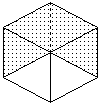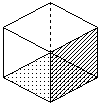
全部で、84×6=504 通りですが、重複して数えたものを除かないといけません。
例えば、下図の青い経路は、2つの面で重複して数えられています。
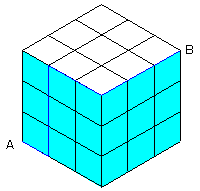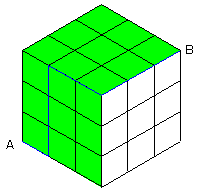
このように、元の立方体の1辺(格子で言うと3つ分)を通る進み方は
2つの面で重複して数えられます。
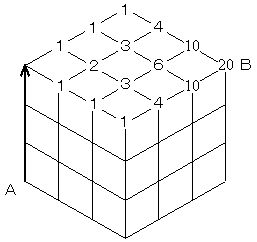
図のように、Aから、立方体の辺のみを通って、3つ進んだあと、
Bに行く行き方は、辺の選び方が3通りあるので、
3×20=60(通り)
同様に、最後に立方体の辺を3つ進んで、Bに行く行き方も 60通り。
合計120通りを引きます。
さらに、面上の線は通らず、立方体の辺だけを通る行き方が6通りありますが、
これは、実は、3つの面で重複して数えられている代わりに、上の120通りの中にも
2回数えられているので、差し引きゼロです。
よって、
504−120=384(通り)
「算数・数学」の部屋に戻る