問題1
4組の夫婦、合計8名の男女が1つの円卓で会食するために、
その座席を抽選によって決める。どの夫婦も隣り合った席に座る確率を求めよ。
解答1
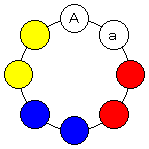
夫婦4組8人をを(A,a),(B,b),(C,c),(D,d)とします。
円順列で考えます。
Aを図の位置に固定しておくと、他の7人が座る方法は
7!=5040 通り ・・・・・・ すべての場合の数
Aの左にaが座った場合(上図)、
赤、青、黄の3つの組に、(B,b),(C,c),(D,d) を割り当てるのは
3!=6通り
B と b の入れかえ、C と c の入れかえ、D と d の入れかえで
2×2×2=8通り
合計 6×8=48通り
a が A の右に座った場合も同様に、48通り
よって、求める確率は
48×2/5040=2/105
問題2
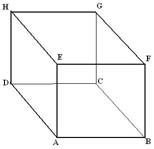
図のような立方体ABCD−EFGHにおいて、辺上を動くPがある。
Pが頂点Aを出発し他の頂点を全て一度だけ通りAに戻る方法は何通りあるか?
解答2
第1手目にAからBに行く、Dに行く、Eに行くのは、その後の進み方は同数あるので、
Eに行くことだけを考えて、あとで3倍する。
さらに、Eに行ったあと、Fに行く、Hに行くのは、同様に同数あるので、Hに行くことだけ
考えて、最後に6倍することにする。
A−E−H−D
と行くと、このあと、C−G−F−B−A と行くしかない。
A−E−H−G
と行くと、このあと、F−B−C−D−A と行くしかない。
よって、
2×6=12通り
算数・数学の部屋に戻る