問題
ある果物や屋にミカン、リンゴ、ナシがそれぞれたくさん並べられている。
この中から8個の果物を選ぶ。ただし、同種の果物については区別がないものとする。つぎのア〜コを求めよ。
(1)どの果物も少なくとも2個は選ぶとき、そのような選び方は全部でア通りある
また8個の果物を選ぶ選び方は全部でイウ通りある。このうち、同種のくだものを6個以上含まない選び方は全部でエオ通りあ る。
(2)ミカン4個、リンゴ2個、ナシ2個を選んだとき、選んだ8個を1列に並べる並べ方は全部でカキク通りある。
またこの8個を円形に並べるとき、その並べ方は全部でケコ通りある。
解答
(1)重複組み合わせを参照してください。
2H3=4C2=6(通り) ア=6
8H3=10C8=45(通り) イウ=45
6個以上含む場合を考える。
6,1,1と選ぶ方法は、3通り。
6,2,0と選ぶ方法は、6通り。
7,1,0と選ぶ方法は、6通り。
8,0,0と選ぶ方法は、3通り。
45−(3+6+6+3)=27(通り) エオ=27
(2)すべての果物を区別するとすると、8個の並べ方は 8!通り。
このうち、ミカンの並べ方4!通り、リンゴの並べ方2!通り、ナシの並べ方2!通りは、
区別しないので、 8!÷(4!×2!×2!)=420(通り) カキク=420
リンゴ2個の位置は次の4通り。
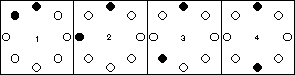
1〜3について、ミカンとナシの並び方は 6!÷(4!×2!)=15(通り)
4について、ナシ2個を
同じ側に2個置く方法:3C2=3(通り)
左右1個ずつ置く方法:以下の6通り

以上より、
3×15+6=51(通り) ケコ=51
「算数・数学」の部屋に戻る