問題
表に1、裏に2と書いてある硬貨を回投げて、
1回目に出る数をx、2回目に出る数をyとして、
座標平面上の点(x,y)を決める。
この試行を独立に2回繰り返して決まる2点と点(0,0)とで
決まる図形(三角形または線分)について
(1)図形が線分になる確率を求めよ。
(2)図形の面積の期待値を求めよ。但し、線分の面積は0とする。
解答
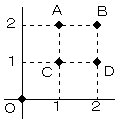
(x、y)で、決まる点は、
A(1,2),B(2,2),C(1,1),D(2,1) の4通りで、
2回繰り返して決まる2点の組合せは、
(A,A)(A,B)(A,C)(A,D)
(B,A)(B,B)(B,C)(B,D)
(C,A)(C,B)(C,C)(C,D)
(D,A)(D,B)(D,C)(D,D)
の16通りです。(カッコ内は順に1回目、2回目の点を表します)。
(1) 図形が線分になるのは、上の16通りのうち、
(A,A)(B,B)(C,C)(D,D)・・・・1回目と2回目が同じ点
(B、C)(C、B)・・・・1回目と2回目が別の点
の6通りです。よって、求める確率は、
6/16=3/8
(2) 上の16通りにおいて、面積は、順に
0 , 1 ,0.5,1.5
1 , 0 , 0 , 1
0.5, 0 , 0 ,0.5
1.5, 1 ,0.5, 0
で、それぞれ起こる確率は 1/16 なので、
(1+0.5+1.5+1+1+0.5+0.5+1.5+1+0.5)/16=9/16
「算数・数学」の部屋に戻る