問題
袋の中にn個(n≧4)の球が入っている。
このうち3個は赤球で、残りの(n−3)個は白球である。
この袋から1個ずつ球を取り出す試行を考える。ただし、取り戻した球は元へ戻さない。
赤球を3個取り出したら、そこで試行は終わるものとする。
試行が終わるまでに取り出した球の総数を表す確率変数をXとし、X=kとなる確率をPkとする。
このときのP3、P4、PkとXの期待値を求めなさい。
解答
3回で試行が終わる ●●● の1通り
1個目に赤が出る確率は 3/n
2個目に赤が出る確率は 2/(n−1)
3個目に赤が出る確率は 1/(n−2)
よって、
P3=6/n(n−1)(n−2)
4回で試行が終わる ○●●● ●○●● ●●○● の3通り
○●●●の確率=(n−3)/n×3/(n−1)×2/(n−2)×1/(n−3)
=6(n−3)/n(n−1)(n−2)(n−3)
●○●●の確率=3/n×(n−3)/(n−1)×2/(n−2)×1/(n−3)
=6(n−3)/n(n−1)(n−2)(n−3)
●●○●の確率=3/n×2/(n−1)×(n−3)/(n−2)×1/(n−3)
=6(n−3)/n(n−1)(n−2)(n−3)
よって、
P4=18(n−3)/n(n−1)(n−2)(n−3)
=18/n(n−1)(n−2)
k回で試行が終わるとき、k個目は赤球であるが、他の2個の赤球は、
k個目以外のk−1個の中のどこにあってもいいので、k-1C2 通りある。
そのうちの1通りの起こる確率の
(分子)=3・2・1・(n−3)(n−4)・・・{n−(k−1)}
(分母)=n(n−1)(n−2)(n−3)・・・{n−(k−1)}
よって、
Pk=k-1C2×6/n(n−1)(n−2)
=3(k−1)(k−2)/n(n−1)(n−2)
=3(k2−3k+2)/n(n−1)(n−2)
Xの期待値は ※k=1,k=2のとき Pk=0 なので、k=1〜nの和を取っても良い。
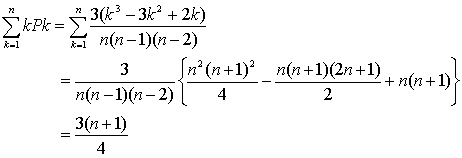
算数・数学の部屋に戻る