丂丂丂丂俙2亜BC偐偮AC亜B2側傜偽丄A亗B偲側傞丅
乮侾乯丂乮俀倶亅俁乯乮亅倶亅侾乯亞侽
乮俀乯丂倶亙俀倶亅俁亙俋
2師曽掱幃z2亖1偺夝偼z亖+1丄-1偱偁傝丄2師曽掱幃z2亖-1偺夝偼z亖+i丄-i偱偁傞丅
偦偙偱丄2師曽掱幃z2亖i偺夝傪媮傔偨偄丅
丂z亖倰乮cos兛+isin兛乯丂
乮倰丄兛偼幚悢偱丄倰亞0丄0亝兛亙2兾乯偲抲偔偲偒丄師偺奺栤偄偵摎偊傛丅
丂乮1乯倰乮cos兛+倝sin兛乯亖倝傪枮偨偡傛偆偵丄掕悢倰丄兛偺抣傪媮傔傛丅
丂乮2乯倸2亖倎cos乮倐兛乯+倝們sin乮倓兛乯傪枮偨偡傛偆偵丄幚悢倎丄倐丄們丄倓偺抣傪媮傔傛丅
丂乮3乯2師曽掱幃倸2亖倝傪枮偨偡傛偆偵丄倰丄兛偺抣傪傕偲傔傛丅
丂乮4乯2師曽掱幃倸2亖倝偺夝傪媮傔傛丅
(侾)Z偺愨懳抣偼偄偔傜偐丠
(俀)Z4偑幚悢偲側傞傛偆側幚悢X偼壗屄偁傞偐丅傑偨偦偺偆偪嵟戝偺傕偺偼壗偐丅
丂嚁(n=1乣23)zn 傪媮傔傛丅丂丂偨偩偟i偼嫊悢扨埵偲偡傞丅
(2)丂335100-308傪24偱妱偭偨梋傝偼偄偔傜偐丠
暋慺悢丂z=x+yi丂偑捈慄y=1偺忋傪摦偔偲偒丄w=z2偼偳傫側恾宍偵側傝傑偡偐丠
栤戣俀
兛丄兝丂偼丂兛2-2兛兝+4兝2亖侽丂傪枮偨偡丄0偱偼側偄暋慺悢偱偁傞偲偟傑偡丅
(1)丂|兛|/|兝|丂丂傪媮傔側偝偄丅
(2)丂arg 兛-arg兝傪媮傔側偝偄丅
(3)暋慺悢暯柺忋偱兛偺昞偡揰傪A丄兝偺昞偡揰傪B丄尨揰傪
俷偲偡傞偲偒丄嶰妏宍OAB偼偳傫側恾宍偱偡偐丠媮傔側偝偄丅
栤戣俁
師偺曽掱幃偑暋慺悢暯柺忋偱昞偡恾宍傪媮傔側偝偄丅
(1)丂
(2) 乥z-2乥=|z-2i|
(3) |z-i|=3
栤戣係
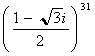 傪媮傔傛丅
傪媮傔傛丅2師晄摍幃丂ax2+x+b>0偺夝偑-1/3<x<1/2偺偲偒丄a,b偺抣傪媮傔傛丅
傑偨丄2師晄摍幃x2+bx+a<0傪夝偗丅
栤戣俀
ax2+(a-1)x+a-1<0 偺晄摍幃偑偡傋偰偺悢x偵懳偟偰惉傝棫偮偨傔偺丄掕悢a偺抣偺斖埻傪媮傔傛丅
栤戣俁
0亝x亝4偱丄偮偹偵晄摍幃x2-6x+a+5<0偑惉傝棫偮傛偆偵丄掕悢a偺抣偺斖埻傪掕傔傛丅
栤戣係
x2+ax+3-a=0偲x2+(3-a)x+a=0偺偆偪偺1偮偺曽掱幃偼夝傪傕偪丄懠偺曽掱幃偼夝傪傕偨側偄偲偒丄掕悢a偺抣偺斖埻傪媮傔傛丅
2師曽掱幃x2-(m-10)x+m+14=0偺堎側傞2偮偺夝偑丄偲傕偵晧偵側傞m偺斖埻偼仩<m<仩偱偁傞丅
栤戣俀
2師曽掱幃x2-ax+a2-4=0偵偮偄偰丄
(1)2偮偺夝偑偲傕偵惓偱偁傞偨傔偺a偺斖埻傪媮傔傛丅
(2)1偮偺夝偩偗偑惓偱偁傞偨傔偺a偺斖埻傪媮傔傛丅
栤戣俁
2師曽掱幃4x2-2ax+1=0偺堎側傞2偮偺夝偑偲傕偵0<x<1偺斖埻偵偁傞偨傔偺掕悢a偺抣偺斖埻傪媮傔傛丅
傑偢2恖偑懳愴偟丄埲崀偦偺彑幰偲偦偺偲偒媥傒偺幰偑師偵懳愴偟偰偄偔丅
偦偺寢壥丄A偼60夞丄B偼40夞僎乕儉傪偟偨丅
偙偺偲偒丄C偺僎乕儉夞悢偺嵟彫抣偲嵟戝抣偼偦傟偧傟偄偔傜偐丅
乮偨偩偟 z~ 偼 z 偺嫟栶暋慺悢丅z~=x-yi乯