問題
iを虚数単位とする。実数Xに対し、Z=(1+Xi)/(1-Xi)とおく。
(1)Zの絶対値はいくらか?
(2)Z4が実数となるような実数Xは何個あるか。またそのうち最大のものは何か。
解答1(計算のみで解く方法)
(1)
Z=(1+Xi)/(1-Xi)
の両辺に (1+Xi) を掛けて
Z=(1+Xi)2/(1+X2)
=(1-X2+2Xi)/(1+X2)
|Z|=√{(1-X2)2+(2X)2}/(1+X2)
=√(1+2X2+X4)/(1+X2)
=1
(2)
(1+X2)Z=(1-X2+2Xi)
2乗して
(1+X2)2Z2=(1-X2+2Xi)2
={(1-X2)2-4X2+4X(1-X2)i}
={(1-6X2+X4)+4X(1-X2)i}
さらに2乗して
(1+X2)4Z4={(1-6X2+X4)2-16X2(1-X2)2+8X(1-X2)(1-6X2+X4)i}
これの虚数部が0になればいいので、
X(1-X2)(1-6X2+X4)=0
X=0,X=±1 はすぐ求められる。
1-6X2+X4=0
より、
X2=3±2√2
X=±√(3±2√2)=√2±1,-√2±1
以上7個。最大のものは √2+1。
解答2(複素平面を使う方法)
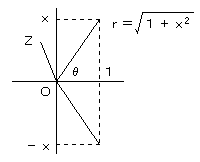
(1)
図のように、1+Xi と 1-Xi を、複素平面上に書きます。
ただし、 −π/2<θ<π/2
1+Xi=reiθ
1-Xi=re-iθ
より、
Z=(r/r)eiθ-(-iθ)=e2iθ
より、
Zは絶対値1、偏角2θの複素数になります。
(2)
Z4=e8iθ=cos(8θ)+isin(8θ)
より、8θ=nπとなるθを求めます。
−π/2<θ<π/2
の範囲でこれを解くと、
θ=-3π/8,-π/4,-π/8,0,π/8,π/4,3π/8
の7個
x=tanθより、xが最大になるのは、θ=3π/8 のとき。
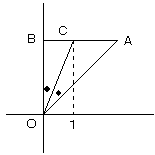
上図において、△OABは、OB=ABの直角二等辺三角形です。
OBが求めるxの値になります。
角の二等分線の定理より、
BC:CA=OB:OA=1:√2
BC=1より、CA=√2
OB=AB=BC+CA=1+√2
算数・数学の部屋に戻る