里奈さんからの質問１２

問題１
複素数　z=x+yi
が直線y=1の上を動く
とき、w=z²はどんな
図形になりますか？

解答１
常にｙ＝１ なので、
　ｚ＝ｘ＋ｉ
と書けます。
　ｗ＝ｚ²＝(ｘ＋ｉ)²＝ｘ²−１＋２ｘｉ
実部を　Ｘ＝ｘ²−１
虚部を　Ｙ＝２ｘ
とおくと、ｘ＝Ｙ/２　より、
　Ｘ＝(Ｙ/２)²−１

グラフはあとまわし。

問題２
α、β　は　
　α²-2αβ+4β²＝０
を満たす、0ではない
複素数であるとします。
(1)　|α|/|β|　　を求めなさい。
(2)　arg α-argβを求めなさい。
(3)複素数平面上でαの表す点をA、βの表す点をB、原点を
Ｏとするとき、三角形OABはどんな図形ですか？求めなさい。

解答２
　α/β＝|α|/|β|ｅ^{ｉ(argα−argβ)}　である。
　つまり、
　α＝|α|(cosθ＋ｉsinθ)、β＝|β|(cosφ＋ｉsinφ)
と書くとき、
　argα＝θ、argβ＝φ　であり、
　α/β＝|α|/|β|｛cos(θ−φ)＋ｉsin(θ−φ)｝
と書けます。
(1)
　α²-2αβ+4β²＝０
の両辺をβ²で割って、
　(α/β)²-2(α/β)+４＝０
　Ｘ＝α/β とおくと、
　Ｘ²−２Ｘ＋４＝０
これを解いて
　Ｘ＝１±√3ｉ
　｜Ｘ｜＝|α/β|＝|α|/|β|＝√(１＋√3²)＝√４＝２・・・答え
(2)
　Ｘ＝１±√3ｉ＝２(cos(±60°)＋ｉｓｉｎ(±60°))　（複号同順）
より、
　arg α-argβ＝±60°・・・答え
(3)
(1)(2) の結果より、
　１つの角が60°で、それをはさむ辺の長さの比が　１：２　である三角形、
　つまり、３つの角が30°、60°、90°の直角三角形で、60°の角が原点にある。

問題３
次の方程式が複素数平面上で
表す図形を求めなさい。
(1)　
(2) ｜z-2｜=|z-2i|
(3) |z-i|=3

解答３
ｚ＝ｘ＋ｙｉとおきます。（ただし、ｘ、ｙは実数）
(1)
　（ｘ＋ｙｉ）−（ｘ−ｙｉ）＝２ｙｉ＝４ｉ
より、
　ｙ＝２　（ｘは任意）
直線　ｙ＝２　（ｘ軸に平行な直線）を表す。

(2)
　｜ｚ−２｜＝｜ｚ−２ｉ｜より、
　｜ｚ−２｜²＝｜ｚ−２ｉ｜²
　｜ｚ−２｜²＝｜（ｘ−２）＋ｙｉ｜²＝（ｘ−２）²＋ｙ²
　｜ｚ−２ｉ｜²＝｜ｘ＋（ｙ−２）ｉ｜²＝ｘ²＋（ｙ−２）²
よって、
　（ｘ−２）²＋ｙ²＝ｘ²＋（ｙ−２）²
　−４ｘ＋４＝−４ｙ＋４
　ｙ＝ｘ
　直線　ｙ＝ｘ　を表す。

(3)
　｜ｚ−ｉ｜²＝９　より、
　｜ｚ−ｉ｜²＝｜ｘ＋（ｙ−１）ｉ｜²＝ｘ²＋（ｙ−１）²＝９
よって、円 ｘ²＋（ｙ−１）²＝９　を表す。

問題４
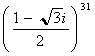を求めよ。

解答４
　ｚ＝(1/2)−(√3/2)ｉ　とおくと、
　ｚ＝cos(-60°)＋ｉｓｉｎ(-60°) と書けます。
　｜ｚ｜＝１　なので、
　ｚ²＝cos(-60°×２)＋ｉｓｉｎ(-60°×２)
　ｚ³＝cos(-60°×３)＋ｉｓｉｎ(-60°×３)
　　　・・・・・・
　ｚ⁶＝cos(-60°×６)＋ｉｓｉｎ(-60°×６)＝１
よって、
　ｚ³⁰＝(ｚ⁶)⁵＝１
　ｚ³¹＝ｚ＝(1/2)−(√3/2)ｉ　

算数・数学の部屋に戻る