問題
複素数 z=x+yi(x>0、y>0)が|z|=2の条件を満たしながら複素数平面を動くとき、
3点 z、z~、1/z を頂点とする三角形の面積の最大値と、そのときの z を求めよ。
(ただし z~ は z の共役複素数。z~=x-yi)
解答1
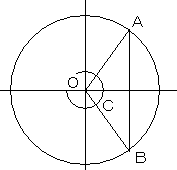
z、z~、1/z の表す点をそれぞれA,B,Cとすると、それぞれの点は上図のような位置関係にあります。
BC=(3/4)OB
より、
△ABC=(3/4)△ABO
であり、△ABOの面積は、OAを対角線とする長方形(辺がx軸、y軸に平行)に等しいので、
△ABO=xy
x>0、y>0 より、相加・相乗平均の関係より、
√xy≦(x+y)/2
であり、等号はx=yのとき。
よって、△ABCが最大となるのは、点Aが偏角45°のときであり、
z=√2+√2i
△ABCの面積は 3/2
解答2
z、z~、1/z の表す点をそれぞれA,B,Cとします。
z の偏角をθ とすると、z、z~、1/z はそれぞれ、
z=2(cosθ+i sinθ)
z~=2(cosθ−i sinθ)
1/z=(1/2)(cosθ−i sinθ)
と書けます。
△ABCにおいて、ABを底辺としたときの高さ(点CからABに下ろした垂線)をhとすると、
AB=4sinθ
h=(3/2)cosθ
であるので、△ABCの面積Sは、
S=AB・h/2=3sinθcosθ=(3/2)sin2θ
0<θ<90° より、Sが最大となるのは、2θ=90°、つまりθ=45°のとき。
このとき、S=3/2 であり、z=√2+√2i
「算数・数学」の部屋に戻る