問題1
2次不等式 ax2+x+b>0の解が-1/3<x<1/2のとき、a,bの値を求めよ。
また、2次不等式x2+bx+a<0を解け。
解答1
2次関数のグラフで、-1/3<x<1/2 の範囲だけ正になっているグラフを思い浮かべると、
以下のようなものが思いつく。
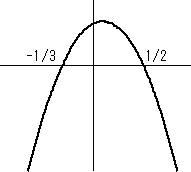
よって、ax2+x+b=0 の解は、x=-1/3, 1/2 なので、
ax2+x+b=a(x+1/3)(x-1/2)
と書ける。展開して、
(右辺)=ax2-ax/6-a/6
ax2+x+b と比較して、a=-6, b=1
このとき、
x2+bx+a<0 は、x2+x-6<0 となり、(x-2)(x+3)<0 より -3<x<2
問題2
ax2+(a-1)x+a-1<0 の不等式がすべての数xに対して成り立つための、定数aの値の範囲を求めよ。
解答2
y=ax2+(a-1)x+a-1 のグラフが、すべてのxについて、x軸より下にあるので、下のようなグラフになる。
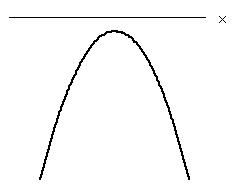
このグラフの特徴として、
・上に凸である。
・x軸と共有点を持たない
これらは式で書くとそれぞれ
a<0 ………(1)
判別式:(a-1)2-4a(a-1)<0 ………(2)
と書ける。(2)より、
(a-1)(-3a-1)<0
(a-1)(3a+1)>0
これより、
a<-1/3 または a>1
ただし、a<0 より、 a<-1/3
問題3
0≦x≦4で、つねに不等式x2-6x+a+5<0が成り立つように、定数aの値の範囲を定めよ。
解答3
y=f(x)=x2-6x+a+5 のグラフは、下に凸である
このグラフが 0≦x≦4 の範囲で常にx軸より下にあるので、図のようなグラフになる。
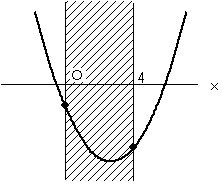
こうなるためには、x=0 のとき、およびx=4 のときのyの値(上図の●)が負であればよい。
f(0)=a+5<0 より、a<-5
f(4)=a-3<0 より、a<3
以上より、 a<-5
問題4
x2+ax+3-a=0とx2+(3-a)x+a=0のうちの1つの方程式は解をもち、他の方程式は解をもたないとき、定数aの値の範囲を求めよ。
解答4
判別式をとったとき、一方が負で他方が非負であればいいので、
a2-4(3-a)≧0 かつ (3-a)2-4a<0 ………(1)
または
a2-4(3-a)<0 かつ (3-a)2-4a≧0 ………(2)
(1) より、
(a≦-6 または a≧2) かつ 1<a<9
よって、
2≦a<9
(2) より、
-6<a<2 かつ (a≦-1 または a≧9)
よって、
-6<a≦1
以上より、 -6<a≦1 または 2≦a<9
算数・数学の部屋に戻る