問題1
2次方程式x2-(m-10)x+m+14=0の異なる2つの解が、ともに負になるmの範囲は□<m<□である。
問題2
2次方程式x2-ax+a2-4=0について、
(1)2つの解がともに正であるためのaの範囲を求めよ。
(2)1つの解だけが正であるためのaの範囲を求めよ。
問題3
2次方程式4x2-2ax+1=0の異なる2つの解がともに0<x<1の範囲にあるための定数aの値の範囲を求めよ。
解答
この手の問題は、
・条件を満たすグラフはどんな位置にあるか?そのための条件は?
・ポイントは、判別式、軸、境界線での値
です。
解答1
f(x)=x2-(m-10)x+m+14 とおきます。
2解がともに負になるのは、
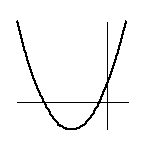
このようなグラフです。
(1)
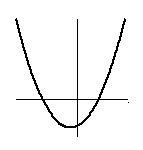 (2)
(2)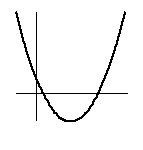 (3)
(3)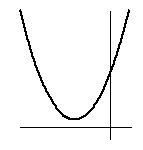
こういうのはダメです。
(1) のようにならないためには、f(0)>0 でなければなりません。
それを満たしたとしても (2) のようになるかも知れないので、そうならないためには、
軸:x=(m-10)/2<0
それも満たしても、(3) のようになるかも知れないので、そうならないためには、
判別式が正でなければなりません。
以上より、
f(0)=m+14>0
(m-10)/2<0
(m-10)2−4(m+14)>0
それぞれ、
m>-14
m<10
m<2 または m>22
よって、-14<m<2
以下は、グラフを自分で描いてください。
解答2
f(x)=x2-ax+a2-4 とおきます。
(1)
f(0)=a2-4>0
軸:a/2>0
判別式:a2−4(a2-4)=-3a2+16>0
それぞれ解くと、
a<−2 または a>2
a>0
-4/√3<a<4/√3(≒2.3)
以上より、
2<a<4/√3
(2)
2解が正と負であるとき、満たすべき条件は
f(0)<0
だけです。これさえ満たせば、判別式は自動的に正になるし、
軸の位置に関係なく、2解は正と負に分かれます。
よって、
f(0)a2-4<0
よって、 −2<a<2
2解が0と正であるとき、
x=0 を代入すると、
a2-4=0
より、a=±2
このとき、f(x)=x2-ax=x(x-a) と書け、
2解は、x=0 と x=a になります。
条件(1つの解が正)より、a>0。よって、a=2
以上より、
−2<a≦2
解答3
f(x)=4x2-2ax+1 とおきます。
満たすべき条件は、
f(0)=1>0
f(1)=−2a+5>0
軸:a/4 が0と1の間になる。つまり 0<a/4<1
判別式:a2−4>0
それぞれ解くと、
a<5/2
0<a<4
a<−2 または a>2
以上より、
2<a<5/2
算数・数学の部屋に戻る