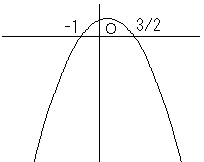
このグラフが y≧0 になるのは -1≦x≦3/2 の範囲です。
答え -1≦x≦3/2
(2x−3)(−x−1) は 2x−3 と −x−1 が掛けられたものです。
2x−3 は、 x=3/2 を境に正と負が分かれます。
−x−1 は、x=-1 を境に正と負が分かれます。
そこで、以下のような表を作ります。
まろさんからの質問
問題 次の不等式を解け。
(1) (2x−3)(−x−1)≧0
(2) x<2x−3<9
解答
(1) y=(2x−3)(−x−1) のグラフは、以下の通りです。
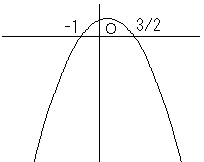
このグラフが y≧0 になるのは -1≦x≦3/2
の範囲です。
答え -1≦x≦3/2
(2x−3)(−x−1) は 2x−3 と −x−1
が掛けられたものです。
2x−3 は、 x=3/2 を境に正と負が分かれます。
−x−1 は、x=-1 を境に正と負が分かれます。
そこで、以下のような表を作ります。
| xの値 | x<−1 | −1 | −1<x<3/2 | 3/2 | 3/2<x |
| −x−1 の値 | + | 0 | − | − | − |
| 2x−3 の値 | − | − | − | 0 | + |
| (2x−3)(−x−1)の値 | − | 0 | + | 0 | − |
この表より、(2x−3)(−x−1)≧0
となるのは、-1≦x≦3/2 であることが分かります。
普通は、下のような下に凸のグラフに変形して
(x−a)(x−b)<0 ならば a<x<b
(x−a)(x−b)>0 ならば x<a または b<x
という形に持っていきます。(ただし、a<b)(等号は必要に応じてつける)
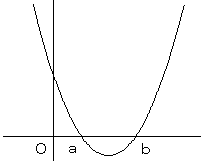
(2x−3)(−x−1)≧0 の場合は、両辺に−1を掛けて(不等号が逆になることに注意)
(2x−3)(x+1)≦0 とし、-1≦x≦3/2 が得られます。
以上、「グラフを書いて調べる」「掛けられている2つの式の正負で調べる」「一般的な形(下に凸)に変形する」
の方法を書きました。
(2) x<2x−3<9 は、
x<2x−3・・・(1)
2x−3<9・・・(2)
の2つの不等式が合わさったものです。
(1) より x>3
(2) より x<6
この2つを同時に満たす範囲は、3<x<6 となります。
「算数・数学」の部屋に戻る