質問・問題に答えるコーナー(立体に関する問題)

分野	質問された方	掲載日	質問内容　答えは質問者のお名前をクリック
立体に関する問題
体積	akari さん２	2001/02/10	半径５ｃｍの球に外接する （１）直円柱 （２）直円錐 （３）正四角錐 の体積を求めなさい。
回転体	yui*さん	2001/08/05	AB=14,AD=7 の、長方形ABCDが、CD上の点Oを中心とする半径6 の円によって切り取られている。 円OとADの交点をEとすると、∠EOD=30°である。 この図形を直線CDを軸として一回転させてできた立体を、軸に平行で、軸から４離れた平面で切ったとき、切り口の面積を求めよ。
四面体の体積	K.Y さん１	2001/11/29	四面体ABCDがある。AB＝BC＝３，BD＝１，AD=２√２，AC=２√５，CD=２√３ である時， (1) その概形を書け。 (2) △ABCの面積S を求めよ。 (3) 四面体ABCDの体積V を求めよ。 (4) 頂点Dから平面ABCに下ろした垂線DHの長さｈを求めよ。
空間図形	独創人（中３）さん１	2002/01/07	直方体ABCD-EFGHがあります。 いま３頂点B,D,Eを通るような平面できります。 対角線AGと平面DBEの交点は線分AGをどのような比に分けますか？
空間図形	B.J さん１	2002/01/17	すべての辺の長さが１の正四角錐のＯ−ＡＢＣＤに対して辺ＯＢ、ＯＤの中点をＰ、Ｑとし、更に平面ＡＰＱと辺ＯＣとの交点をＲとする。このとき、次の問に答えよ。 （１）ＯＲの長さを求めよ。 （２）四角形ＡＰＲＱの面積を求めよ。 （３）四角錐Ｏ−ＡＰＲＱの体積を求めよ。
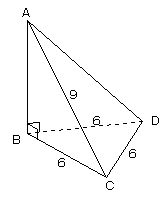
空間図形	里奈さん１０	2002/02/25	底辺が1辺6の正三角形で、ABが高さである三角錐A-BCDがあり、AC＝9である。 この三角錐をABを軸として回転するとき、三角形ACDの通る部分の体積を求めよ。

算数・数学の部屋に戻る