問題
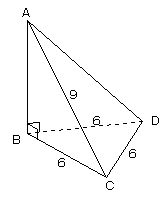
底辺が1辺6の正三角形で、ABが高さである三角錐A-BCDがあり、AC=9である。
この三角錐をABを軸として回転するとき、三角形ACDの通る部分の体積を求めよ。
解答
ABが高さであるので、∠ABC=∠ABD=90°である。
また、△ABCにおける三平方の定理より、
AB=√(92-62)=√45=3√5
この三角錐をABを軸に回転した図は以下の通りである。
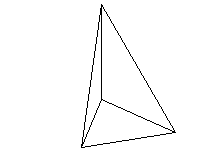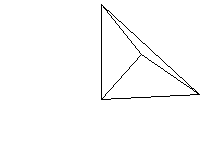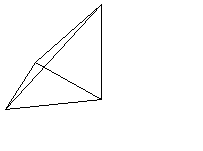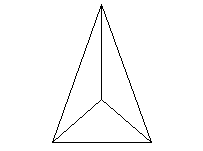
また、これを、軸の方向から見ると、下のようになり、辺CDの通る部分は、
図の、2つの円にはさまれた部分となる。
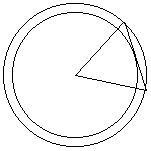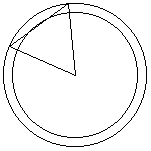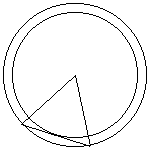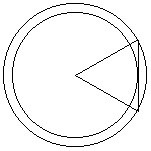
よって、求める立体は、大円を底面とし高さABの円錐から、
小円を底面とし高さABの円錐を引いた立体である。
大円の半径は、BC=6 面積は 36π
小円の半径は、CDの中点をMとするとき、BM=3√3 面積は27π
体積は (36π−27π)×3√5÷3=9√5π
算数・数学の部屋に戻る