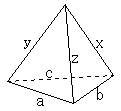問題
四面体ABCDがある。AB=BC=3,BD=1,AD=2√2,AC=2√5,CD=2√3 である時,
(1) その概形を書け。
(2) △ABCの面積S を求めよ。
(3) 四面体ABCDの体積V を求めよ。
(4) 頂点Dから平面ABCに下ろした垂線DHの長さhを求めよ。
解答
(1) 三平方の定理より
∠ADB, ∠ADC は、ともに 直角であることがわかる。
よって、概形は以下のようになる。
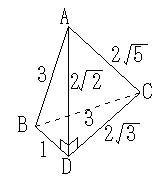
(2) △ABC は二等辺三角形なので、B から AC に下ろした垂線の足を D とすると、D は AC の中点となる。
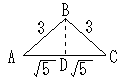
三平方の定理より、BD = 2 が得られるので、
S=(2√5×2)/2=2√5
別解
ヘロンの公式により
S=√{(3+√5)(3-√5)√5・√5}=√20=2√5
(3) △BCD を底面とすると、AD が高さになる。
△BCD の面積は、ヘロンの公式により、
△BCD=√{(2+√3)(2-√3)(√3+1)(√3-1)}=√2 ※余弦定理から求める方法もある
よって、
V=(√2×2√2)/3=4/3
※四面体版ヘロンの公式もありますが、覚えるのも計算も大変です。お勧めしません。
(4) △ABC を底面とすると、h が高さになるので、(2)(3) の結果より、
V=Sh/3
h=3V/S=3×(4/3)/2√5=2√5/5
算数・数学の部屋に戻る