yui*さんからの質問

問題
AB=14,AD=7 の、長方形ABCDが、CD上の点Oを中心とする半径6 の円によって切り取られている。
円OとADの交点をEとすると、∠EOD=30°である。
この図形を直線CDを軸として一回転させてできた立体を、軸に平行で、軸から４離れた平面で切ったとき、
切り口の面積を求めよ。

解答

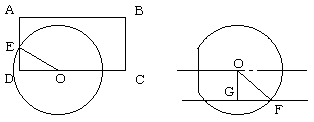
上図において、∠EOD=30°、OE=6 より、ED=3。
これをCDを軸に回転させた立体を、軸に平行で、軸から４離れた平面で切ると、
右の図のようになります。
この切り口は、ED を含む平面と重なっていないので、結局、半径６の球を中心から
４の位置で切ったのと同じで、切り口は円です。
右の図の△OFG において、∠OGF＝90°、OF＝6、OG＝4 より、
　FG²＝6²-4²＝20
よって、切り口の円の面積は、
　π×FG²＝20π　（πは円周率）

「算数・数学」の部屋に戻る