問題
すべての辺の長さが1の正四角錐のO−ABCDに対して辺OB、ODの中点をP、
Qとし、更に平面APQと辺OCとの交点をRとする。このとき、次の問に答えよ。
(1)ORの長さを求めよ。
(2)四角形APRQの面積を求めよ。
(3)四角錐O−APRQの体積を求めよ。
解答
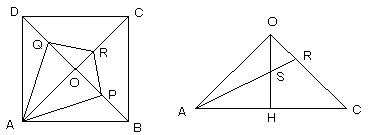
図の左は底面ABCDに垂直な方向から見た図、
図の右は△ACOの断面図で、HはACの中点、SはOHの中点で、
ARとPQの交点がSになります。
(1)
上図右において、メネラウスの定理より、
OS・HA・CR=SH・AC・RO
CR:RO=2:1
よって、OR=OC/3=1/3
(2)
上図右の△AHSにおいて、
AH:HS=2:1
より、
AS=HS×√5
HS=√2/4 なので、
AS=√10/4
ARはASの4/3倍(メネラウスで示しても良いし、RからACに垂線を下ろしても良い)
なので、
AR=√10/3
一方、PQ=BC/2=√2/2
ARとPQは垂直なので、
四辺形APRQ=AR・PQ÷2=√5/6
(3)
この立体を、△OPQが底面でRをもう一つの頂点とする三角錐Aと、
同じく△OPQが底面で、Aをもう一つの頂点とする三角錐Bに分けて考えます。
△OPQの面積は、OP×OQ÷2=1/8
上図右のHAが三角錐Bの高さで、三角錐Aの高さはこれの1/3倍なので、
結局、AHの 4/3 倍の高さの三角錐と同じ体積である。
AH×4/3=√2/2×4/3=2√2/3
四角錐O−APRQ=△OPQ×2√2/3÷3=√2/36
算数・数学の部屋に戻る