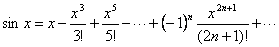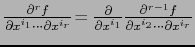|
|||||||||
| 名前:ShoWat 日付:7月31日(火) 22時22分 | |||||||||
|
|
|||||||||
| 名前:hikami 日付:7月31日(火) 1時43分 | |||||||||
|
|
|||||||||||||||||||||
| 名前:ShoWat 日付:7月30日(月) 21時45分 | |||||||||||||||||||||
|
|
|||||||||
| 名前:INI 日付:7月30日(月) 20時40分 | |||||||||
|
|
|||||
| 名前:ピーター 日付:7月29日(日) 21時37分 | |||||
|
|
|||||||||
| 名前:ShoWat 日付:7月29日(日) 18時19分 | |||||||||
|
|
|||||||||||||||||||||
| 名前:teru 日付:7月29日(日) 13時44分 | |||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||
| 名前:やすし 中学1年 日付:7月29日(日) 10時5分 | |||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||
| 名前:ShoWat 日付:7月28日(土) 21時30分 | |||||||||||||||||
|
|
|||||||||
| 名前:コスモス 日付:7月28日(土) 19時54分 | |||||||||
|
|
|||||
| 名前:やすし 日付:7月28日(土) 18時35分 | |||||
|
|
|||||
| 名前:教得手 学 日付:7月28日(土) 13時56分 | |||||
|
|
||
| 名前:大学三年 日付:7月28日(土) 13時50分 | ||
|
|
|||||
| 名前:大学1年 日付:7月28日(土) 11時44分 | |||||
|
|
|||||||||||||||||||||||||||||||||||||
| 名前:中3 日付:7月28日(土) 9時4分 | |||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||
| 名前:ゴン 日付:7月27日(金) 23時51分 | |||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||
| 名前:ShoWat 日付:7月27日(金) 22時8分 | |||||||||||||||||||||||||||||||||
|
|
|||||
| 名前:村の人々 日付:7月27日(金) 21時15分 | |||||
|
|
|||||
| 名前:太郎 日付:7月27日(金) 20時48分 | |||||
|
|
|||||
| 名前:tomato 日付:7月27日(金) 20時35分 | |||||
|
|
||
| 名前:けん 日付:7月27日(金) 12時9分 | ||
|
|
|||||||||
| 名前:MONO消しゴム 日付:7月27日(金) 8時52分 | |||||||||
|
|
|||||||||||||
| 名前:Nanami 日付:7月26日(木) 23時0分 | |||||||||||||
|
|
|||||
| 名前:MONO消しゴム 日付:7月26日(木) 21時56分 | |||||
|
|
|||||||||
| 名前:おばけ 日付:7月26日(木) 21時37分 | |||||||||
|
|
|||||||||
| 名前:高3 日付:7月26日(木) 20時30分 | |||||||||
|
|
|||||||||||||
| 名前:みかげ 中3 日付:7月26日(木) 19時59分 | |||||||||||||
|
|
|||||||||
| 名前:みかげ 中3 日付:7月26日(木) 19時51分 | |||||||||
|
|
|||||
| 名前:みかげ 中3 日付:7月26日(木) 17時23分 | |||||
|
|
|||||||||||||
| 名前:みかげ 中3 日付:7月26日(木) 16時46分 | |||||||||||||
|
|
|||||||||
| 名前:おふくろさん 日付:7月26日(木) 15時45分 | |||||||||
|
|
|||||||||
| 名前:INI 日付:7月26日(木) 2時22分 | |||||||||
|
|
|||||||||
| 名前:フラッシュ 高2 日付:7月25日(水) 21時35分 | |||||||||
|
|
|||||||||
| 名前:ラズマリー 日付:7月25日(水) 20時55分 | |||||||||
|
|
|||||||||||||||||
| 名前:ShoWat 日付:7月25日(水) 18時18分 | |||||||||||||||||
|
|
|||||||||||||||||||||||||
| 名前:マリオ 日付:7月25日(水) 1時28分 | |||||||||||||||||||||||||
|
|
|||||
| 名前:コスモス 日付:7月24日(火) 20時59分 | |||||
|
|
|||||||||
| 名前:すう 高校3年 日付:7月24日(火) 19時46分 | |||||||||
|
|
|||||
| 名前:ShoWat 日付:7月24日(火) 18時21分 | |||||
|
|
||
| 名前:L.A 日付:7月24日(火) 14時9分 | ||
|
|
|||||||||
| 名前:INI 日付:7月23日(月) 22時12分 | |||||||||
|
|
|||||||||||||
| 名前:やすし 日付:7月23日(月) 18時3分 | |||||||||||||
|
|
|||||||||
| 名前:nijiiro darkness 日付:7月22日(日) 21時49分 | |||||||||
|
|
|||||||||||||
| 名前:ShoWat 日付:7月22日(日) 21時23分 | |||||||||||||
|
|
|||||||||||||
| 名前:K 日付:7月22日(日) 20時4分 | |||||||||||||
|
|
|||||||||
| 名前:Ini 日付:7月22日(日) 19時55分 | |||||||||
|
|
|||||||||
| 名前:ShoWat 日付:7月22日(日) 17時5分 | |||||||||
|
|
|||||
| 名前:ShoWat 日付:7月22日(日) 15時49分 | |||||
|
|
|||||||||
| 名前:ShoWat 日付:7月22日(日) 15時14分 | |||||||||
|
|
|||||||||
| 名前:ShoWat 日付:7月22日(日) 14時58分 | |||||||||
|
|
|||||||||||||
| 名前:Grade7 日付:7月22日(日) 14時15分 | |||||||||||||
|
|
|||||||||||||
| 名前:K 日付:7月22日(日) 1時14分 | |||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||
| 名前:コスモス 日付:7月21日(土) 21時46分 | |||||||||||||||||||||||||||||||||||||
|
|
|||||||||
| 名前:IGA(浪1) 日付:7月21日(土) 21時31分 | |||||||||
|
|
||
| 名前:コスモス 日付:7月21日(土) 19時16分 | ||
|
|
|||||||||||||
| 名前:ユイ 日付:7月21日(土) 16時9分 | |||||||||||||
|
|
|||||||||||||
| 名前:√ 日付:7月21日(土) 14時36分 | |||||||||||||
|
|
|||||||||
| 名前:nijiiro darkness 日付:7月20日(金) 22時13分 | |||||||||
|
|
|||||||||||||||||||||||||
| 名前:kazu 日付:7月20日(金) 13時2分 | |||||||||||||||||||||||||
|
|
|||||||||||||||||||||
| 名前:ユイ 日付:7月20日(金) 11時6分 | |||||||||||||||||||||
|
|
||
| 名前:ティ 日付:7月20日(金) 1時42分 | ||
|
|
|||||||||
| 名前:ユイ 日付:7月19日(木) 18時7分 | |||||||||
|
|
|||||||||||||
| 名前:ユイ 日付:7月19日(木) 18時4分 | |||||||||||||
|
|
||
| 名前:コスモス 日付:7月19日(木) 4時43分 | ||
|
|
||
| 名前:コスモス 日付:7月19日(木) 4時35分 | ||
|
|
|||||
| 名前:コスモス 日付:7月19日(木) 3時28分 | |||||
|
|
|||||||||||||
| 名前:ユイ 日付:7月19日(木) 2時19分 | |||||||||||||
|
|
|||||||||
| 名前:ユイ 日付:7月19日(木) 2時18分 | |||||||||
|
|
|||||||||||||||||||||
| 名前:dr 日付:7月19日(木) 0時25分 | |||||||||||||||||||||
|
|
|||||||||||||||||||||||||
| 名前:ShoWat 日付:7月18日(水) 22時0分 | |||||||||||||||||||||||||
|
|
|||||
| 名前:Grade7 日付:7月18日(水) 19時27分 | |||||
|
|
|||||||||
| 名前:フジ 日付:7月18日(水) 16時5分 | |||||||||
|
|
|||||||||
| 名前:フジ 日付:7月18日(水) 15時43分 | |||||||||
|
|
|||||||||||||||||
| 名前:コスモス 日付:7月18日(水) 13時56分 | |||||||||||||||||
|
|
|||||
| 名前:まってぃ 大学一年工学部 日付:7月18日(水) 0時13分 | |||||
|
|
|||||
| 名前:ガガガS 日付:7月17日(火) 21時41分 | |||||
|
|
|||||||||||||
| 名前:なりたて受験生 日付:7月17日(火) 21時8分 | |||||||||||||
|
|
|||||
| 名前:なかたこう 日付:7月17日(火) 17時29分 | |||||
|
|
||
| 名前:音楽の友 日付:7月16日(月) 0時4分 | ||
|
|
|||||||||||||
| 名前:ShoWat 日付:7月15日(日) 21時58分 | |||||||||||||
|
|
|||||||||||||||||
| 名前:zaza 日付:7月15日(日) 7時43分 | |||||||||||||||||
|
|
|||||
| 名前:かんかん 日付:7月14日(土) 22時31分 | |||||
|
|
|||||||||
| 名前:ShoWat 日付:7月14日(土) 21時54分 | |||||||||
|
|
|||||||||||||
| 名前:たぷー @高一 日付:7月14日(土) 19時25分 | |||||||||||||
|
|
|||||||||||||||||||||||||
| 名前:ShoWat 日付:7月14日(土) 12時2分 | |||||||||||||||||||||||||
|
|
|||||
| 名前:ゴン 日付:7月14日(土) 0時40分 | |||||
|
|
|||||
| 名前:やすし 日付:7月13日(金) 19時17分 | |||||
|
|
|||||||||||||||||||||
| 名前:たけひこ@高校2年 日付:7月13日(金) 14時31分 | |||||||||||||||||||||
|
|
|||||||||
| 名前:ウー 日付:7月13日(金) 13時19分 | |||||||||
|
|
|||||||||||||||||
| 名前:けん 日付:7月13日(金) 11時13分 | |||||||||||||||||
|
|
|||||
| 名前:高橋 日付:7月13日(金) 10時44分 | |||||
|
|
|||||
| 名前:高橋 日付:7月13日(金) 10時41分 | |||||
|
|
|||||
| 名前:高校3年生です。 日付:7月13日(金) 9時0分 | |||||
|
|
|||||||||
| 名前:みぉ(高3) 日付:7月13日(金) 4時25分 | |||||||||
|
|
|||||||||
| 名前:ShoWat 日付:7月12日(木) 23時6分 | |||||||||
|
|
|||||
| 名前:高校3年生です。 日付:7月12日(木) 11時10分 | |||||
|
|
|||||||||||||
| 名前:高校3年生です。 日付:7月12日(木) 11時3分 | |||||||||||||
|
|
|||||||||||||
| 名前:高校3年生です。 日付:7月12日(木) 10時53分 | |||||||||||||
|
|
|||||||||
| 名前:高校3年 日付:7月12日(木) 10時49分 | |||||||||
|
|
|||||||||
| 名前:高校3年生 日付:7月12日(木) 0時30分 | |||||||||
|
|
|||||
| 名前:がうす 日付:7月11日(水) 23時23分 | |||||
|
|
|||||
| 名前:ジェン 日付:7月11日(水) 22時27分 | |||||
|
|
|||||
| 名前:めちゃイケナイ 高2 日付:7月11日(水) 20時30分 | |||||
|
|
|||||||||||||||||
| 名前:チョッパ 日付:7月11日(水) 15時50分 | |||||||||||||||||
|
|
|||||||||
| 名前:バンビ 日付:7月11日(水) 12時43分 | |||||||||
|
|
|||||||||||||||||||||
| 名前:高校3年生 日付:7月11日(水) 3時28分 | |||||||||||||||||||||
|
|
|||||
| 名前:グレイス 日付:7月10日(火) 21時52分 | |||||
|
|
|||||||||
| 名前:ゴン 日付:7月10日(火) 20時47分 | |||||||||
|
|
|||||||||||||||||||||
| 名前:√ 日付:7月10日(火) 20時46分 | |||||||||||||||||||||
|
|
|||||
| 名前:やすし 日付:7月10日(火) 20時0分 | |||||
|
|
|||||||||||||||||||||
| 名前:バンビ 日付:7月10日(火) 15時24分 | |||||||||||||||||||||
|
|
|||||||||
| 名前:バンビ 日付:7月10日(火) 12時23分 | |||||||||
|
|
|||||||||
| 名前:こぶ平 日付:7月9日(月) 20時34分 | |||||||||
|
|
|||||||||
| 名前:K'z 日付:7月9日(月) 19時42分 | |||||||||
|
|
|||||
| 名前:えいく 日付:7月9日(月) 19時2分 | |||||
|
|
|||||||||
| 名前:ボス 日付:7月9日(月) 18時59分 | |||||||||
|
|
|||||
| 名前:えちか 日付:7月9日(月) 18時48分 | |||||
|
|
|||||
| 名前:高校1年 日付:7月9日(月) 15時22分 | |||||
|
|
||
| 名前:ゴン 日付:7月8日(日) 22時2分 | ||
|
|
|||||
| 名前:ShoWat 日付:7月8日(日) 18時15分 | |||||
|
|
|||||
| 名前:グラテス ~オカリスの夢~ 日付:7月8日(日) 16時41分 | |||||
|
|
|||||
| 名前:グラテス ~オカリスの夢~ 日付:7月8日(日) 16時37分 | |||||
|
|
|||||||||
| 名前:悟飯 日付:7月8日(日) 1時55分 | |||||||||
|
|
|||||
| 名前:みるく 日付:7月7日(土) 23時59分 | |||||
|
|
|||||
| 名前:TAKU 日付:7月7日(土) 22時46分 | |||||
|
|
|||||
| 名前:中学2年 日付:7月7日(土) 11時45分 | |||||
|
|
|||||||||||||||||||||||||
| 名前:ShoWat 日付:7月7日(土) 0時34分 | |||||||||||||||||||||||||
|
|
||
| 名前:mika 日付:7月6日(金) 22時45分 | ||
|
|
|||||||||||||||||
| 名前:ぐるる 日付:7月6日(金) 22時39分 | |||||||||||||||||
|
|
|||||||||||||
| 名前:バンビ 日付:7月6日(金) 16時8分 | |||||||||||||
|
|
||
| 名前:ゴン 日付:7月5日(木) 23時28分 | ||
|
|
||
| 名前:YM 日付:7月5日(木) 16時13分 | ||
|
|
||
| 名前:YM 日付:7月5日(木) 16時10分 | ||
|
|
||
| 名前:YM 日付:7月5日(木) 16時7分 | ||
|
|
|||||
| 名前:YM 日付:7月5日(木) 16時3分 | |||||
|
|
|||||||||||||||||||||
| 名前:やす 日付:7月5日(木) 12時10分 | |||||||||||||||||||||
|
|
|||||
| 名前:ゴン 日付:7月5日(木) 0時55分 | |||||
|
|
|||||||||||||
| 名前:ぐるる 日付:7月5日(木) 0時30分 | |||||||||||||
|
|
|||||||||||||||||
| 名前:至眞 日付:7月4日(水) 18時11分 | |||||||||||||||||
|
|
|||||||||||||||||||||
| 名前:えれな 17歳 日付:7月4日(水) 6時43分 | |||||||||||||||||||||
|
|
|||||||||
| 名前:音楽の友 日付:7月4日(水) 0時6分 | |||||||||
|
|
|||||||||
| 名前:めちゃイケナイ 高2 日付:7月3日(火) 21時36分 | |||||||||
|
|
|||||||||||||||||||||
| 名前:中3 日付:7月2日(月) 21時36分 | |||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||
| 名前:助けてください 日付:7月2日(月) 15時40分 | |||||||||||||||||||||||||||||||||||||
|
|
|||||||||
| 名前:バンビ 日付:7月2日(月) 13時44分 | |||||||||
|
|
|||||
| 名前:にぱ~☆ 日付:7月1日(日) 21時3分 | |||||
|
|
|||||
| 名前:かな 日付:7月1日(日) 16時59分 | |||||
|
|
|||||||||||||||||||||
| 名前:バンビ 日付:7月1日(日) 16時4分 | |||||||||||||||||||||
|
|
|||||||||||||
| 名前:sakura 日付:7月1日(日) 12時54分 | |||||||||||||
|
|
|||||
| 名前:sakura 日付:7月1日(日) 12時49分 | |||||
|
|
|||||||||
| 名前:ブリーフ 日付:7月1日(日) 12時9分 | |||||||||
|
|
|||||
| 名前:sakura 日付:7月1日(日) 12時1分 | |||||
|

















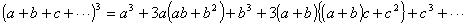

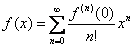 通りなのですが、
通りなのですが、