1. y=m(x−α)(x−β) において、
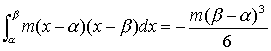
が成り立つ。
証明
y=m(x2+bx+c) とおきます。
ただし b=−(α+β), c=αβ。
積分して、
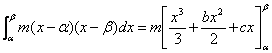
=(m/6){2(β3−α3)+3b(β2−α2)+6c(β−α)}
=(m/6)(β−α){2(β2+αβ+α2)−3(α+β)2+6αβ}
=(m/6)(β−α)(−α2−β2+2αβ)
=−m(β−α)3/6
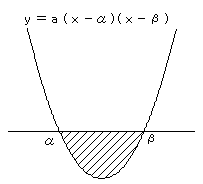
特に、α、βが実数で、α<β であるとき、上記の面積は
m(β−α)3/6
となります。
2次関数の積分公式
1. y=m(x−α)(x−β) において、
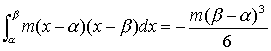
が成り立つ。
証明
y=m(x2+bx+c) とおきます。
ただし b=−(α+β), c=αβ。
積分して、
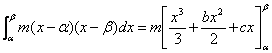
=(m/6){2(β3−α3)+3b(β2−α2)+6c(β−α)}
=(m/6)(β−α){2(β2+αβ+α2)−3(α+β)2+6αβ}
=(m/6)(β−α)(−α2−β2+2αβ)
=−m(β−α)3/6
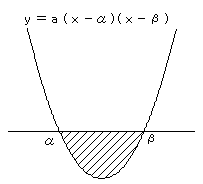
特に、α、βが実数で、α<β であるとき、上記の面積は
m(β−α)3/6
となります。
2.
y=f(x)=ax2+bx+c のグラフと
y=g(x)=dx2+ex+f のグラフが異なる2点で交わるとき、
2つの放物線に囲まれた部分の面積Sは
S=la−dl(β-α)3/6
ただし、α、βは2交点のx座標(α<β)
証明
h(x)=f(x)−g(x)
とすると、求める面積Sは、
![]()
となり、さらに、h(x)=0 の解は x=α、β なので、
h(x)=(a−d)(x−α)(x−β)
と書け、1.の公式がそのまま使えます。
よって、
S=la−dl(β-α)3/6
3.
y=f(x)=ax2+bx+c のグラフをCとし、
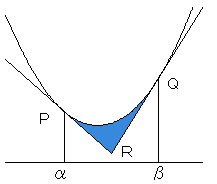
C上の異なる2点(α、f(α))、(β、f(β)) における接線と、Cとで
囲まれた部分の面積Sは
S=|a|(β−α)3/12
で表される。ただし、α<βとする。
証明
P、Qにおける接線を、m、n とすると、m、nの式はそれぞれ
m: y=f'(α)(x−α)+f(α)
n: y=f'(β)(x−β)+f(β)
であり、f'(x)=2ax+b を用いて、交点Rの座標を求めると、
(2aα+b)(x−α)+aα2+bα+c=(2aβ+b)(x−β)+aβ2+bβ+c
2aαx−aα2=2aβx−aβ2
2a(α−β)x=a(α2−β2)
α−β≠0、a≠0 より、両辺 2a(α−β)で割って、
x=(α+β)/2
y=f'(α)(x−α)+f(α) に代入して、
y=aαβ + b(α+β)/2 + c
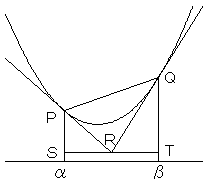
図のように、Rを通って、x軸に平行な直線と、P、Qからx軸におろした垂線との
交点をS、Tとする。
求める面積は
台形PSTQ から △PSR、△QRT、Cと線分PQで囲まれた部分 をひいた部分
の面積となります。
※以下、Cが下に凸として説明します。
PS=aα(α−β) + b(α−β)/2
QT=aβ(β−α) + b(β−α)/2
ST=β−α
より、
台形PSTQ=(PS+QT)ST/2=a(β−α)3/2
Rは、STの中点なので、△PQR は、台形PSTQの半分の面積で、
△PQR=a(β−α)3/4
また、線分PQとCで囲まれた部分は
−a(x−α)(x−β) をαからβまで積分したものなので、1.の公式より
a(β−α)3/6
以上より、求める面積Sは
S=a(β−α)3/4−a(β−α)3/6=a(β−α)3/12
Cが上に凸の場合は、上記のPS、QTおよび、線分PQとCで囲まれた部分の
符号が逆となり、 −a(β−α)3/12 となります。
両者あわせて
S=|a|(β−α)3/12
と表せます。
4.
y=f(x)=ax2+bx+c のグラフをCとし、
C上の点Pにおける接線mと、Pを通らないy軸に平行な直線nがあり、
この2直線とCとで囲まれる部分の面積Sは、
S=|a|(β−α)3/3
と表される。
ただし、接点のx座標と、y軸に平行な直線のxの値の大きい方をβ、他方をαとする。
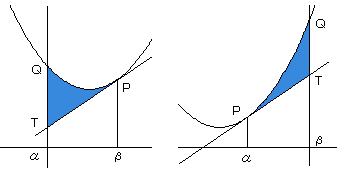
証明
直線nとCの交点をQ、mとnの交点をTとします。
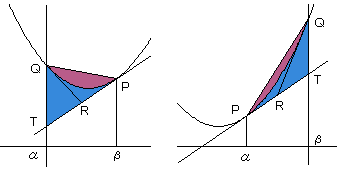
3.の証明過程を踏まえると、点QにおけるCの接線は
PQの中点Rを通ります。
また、1.3.の結果より、
線分PQとCで囲まれた部分の面積は
|a|(β-α)3/6
2線分QR、PRと、CのPからQまでの部分で囲まれた部分の面積は
|a|(β-α)3/12
よって、
△PQR=|a|(β-α)3/6 + |a|(β-α)3/12 = |a|(β-α)3/4
PR=RTより、
△QRT=△PQR=|a|(β-α)3/4
よって、求める面積Sは、
|a|(β-α)3/12+|a|(β-α)3/4=|a|(β-α)3/3