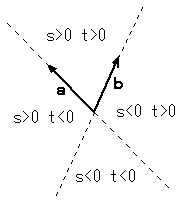
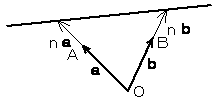
a,b をn倍したベクトルの、
両終点を通る直線上。
特に s+t=1 の時は直線AB上
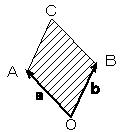
BC=a、AC=b としたとき、
平行四辺形OACBの周上
および内部
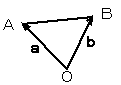
線分AB上。点A、Bを含む

線分AB上。点A、Bを含まない
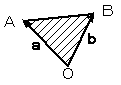
三角形OABの周上
および内部
ベクトルの一次結合
以下、位置ベクトルは、1点Oを始点とするものとします。
太字はベクトルを表します。
平面上において、平行でない2つのベクトルa,b があるとき、
c=sa+tb
を、a,b の一次結合(Linear Combination) と言います。
ここでは、s,t の値によって、c の存在する範囲がどのようになるかをまとめておきます。
| s,t の正負による区分 | s+t=n | 0≦s≦1 0≦t≦1 |
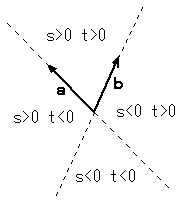 |
 a,b をn倍したベクトルの、 両終点を通る直線上。 特に s+t=1 の時は直線AB上 |
 BC=a、AC=b としたとき、 平行四辺形OACBの周上 および内部 |
| s+t=1 s≧0 t≧0 | s+t=1 s>0 t>0 | 0≦s+t≦1 s≧0 t≧0 |
 線分AB上。点A、Bを含む |
 線分AB上。点A、Bを含まない |
 三角形OABの周上 および内部 |
他にも、いろんなパターンがあります。
算数・数学の部屋に戻る