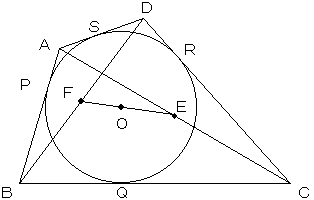
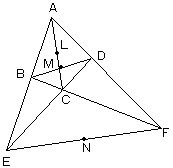
|
|||||
| ���O�F�^���*�f ���t�F11��30��(��) 21��24�� | |||||
|
|
|||||
| ���O�F���� ���t�F11��30��(��) 18��46�� | |||||
|
|
|||||
| ���O�F��݁i���Q�j ���t�F11��30��(��) 16��12�� | |||||
|
|
|||||
| ���O�F�s�b�R�� ���t�F11��30��(��) 16��1�� | |||||
|
|
|||||||||||||||||
| ���O�F��������� ���t�F11��30��(��) 12��31�� | |||||||||||||||||
|
|
|||||||||
| ���O�F���i��w1�N���j ���t�F11��29��(��) 23��31�� | |||||||||
|
|
|||||
| ���O�F����� ���t�F11��29��(��) 22��6�� | |||||
|
|
|||||||||||||||||
| ���O�Fbouzu(�Љ�l) ���t�F11��29��(��) 20��53�� | |||||||||||||||||
|
|
|||||||||||||
| ���O�F�������i���R�j ���t�F11��29��(��) 20��11�� | |||||||||||||
|
|
|||||
| ���O�F����i���R�j ���t�F11��29��(��) 18��17�� | |||||
|
|
|||||
| ���O�F��܂�� ���t�F11��28��(��) 0��54�� | |||||
|
|
|||||
| ���O�Fharu ���t�F11��28��(��) 0��52�� | |||||
|
|
|||||
| ���O�F����i���R�j ���t�F11��27��(��) 14��48�� | |||||
|
|
|||||||||
| ���O�F����i���R�j ���t�F11��27��(��) 13��58�� | |||||||||
|
|
|||||||||
| ���O�F���� ���t�F11��27��(��) 0��34�� | |||||||||
|
|
|||||||||||||
| ���O�Ftomo(���Q) ���t�F11��26��(�y) 11��1�� | |||||||||||||
|
|
|||||||||||||||||||||||||
| ���O�F�I�����W�p���N ���t�F11��26��(�y) 2��33�� | |||||||||||||||||||||||||
|
|
|||||||||||||
| ���O�F�Y�߂�q�r�@ ���t�F11��25��(��) 20��29�� | |||||||||||||
|
|
|||||||||
| ���O�F����i���R�j ���t�F11��25��(��) 19��28�� | |||||||||
|
|
|||||||||||||||||||||
| ���O�F�͂�� ���t�F11��25��(��) 19��20�� | |||||||||||||||||||||
|
|
|||||
| ���O�F���� ���t�F11��24��(��) 23��19�� | |||||
|
|
|||||||||||||
| ���O�F�������i���R�j ���t�F11��24��(��) 20��46�� | |||||||||||||
|
|
|||||
| ���O�F���C�_�[ ���t�F11��24��(��) 16��6�� | |||||
|
|
|||||
| ���O�F���C�_�[ ���t�F11��24��(��) 16��0�� | |||||
|
|
|||||
| ���O�F���C�_�[ ���t�F11��24��(��) 15��55�� | |||||
|
|
|||||
| ���O�F�Ȃ̂͂�ӂ� ���t�F11��24��(��) 12��4�� | |||||
|
|
|||||||||
| ���O�F�� ���t�F11��23��(��) 22��33�� | |||||||||
|
|
|||||
| ���O�Fai ���t�F11��23��(��) 22��22�� | |||||
|
|
|||||||||
| ���O�F�^���*�f ���t�F11��23��(��) 19��1�� | |||||||||
|
|
|||||||||
| ���O�F�s���N�t���C�h ���t�F11��23��(��) 11��5�� | |||||||||
|
|
|||||
| ���O�F���T ���t�F11��21��(��) 19��20�� | |||||
|
|
|||||||||
| ���O�F��{�@���w1�N�ł��B ���t�F11��21��(��) 0��4�� | |||||||||
|
|
|||||||||||||||||||||||||
| ���O�F���ˁ@���Q ���t�F11��20��(��) 21��38�� | |||||||||||||||||||||||||
|
|
|||||||||
| ���O�F���T ���t�F11��20��(��) 17��15�� | |||||||||
|
|
|||||||||
| ���O�F�������đ�O���j������� ���t�F11��20��(��) 14��21�� | |||||||||
|
|
|||||
| ���O�Fhide ���t�F11��20��(��) 0��27�� | |||||
|
|
|||||||||||||||||||||
| ���O�F�֓c ���t�F11��19��(�y) 21��0�� | |||||||||||||||||||||
|
|
|||||||||||||||||
| ���O�FYuma�i���R�j ���t�F11��19��(�y) 16��54�� | |||||||||||||||||
|
|
||
| ���O�F���݂� ���t�F11��19��(�y) 10��27�� | ||
|
|
|||||||||
| ���O�F������� ���t�F11��18��(��) 21��59�� | |||||||||
|
|
|||||||||||||
| ���O�F���w�܂ɂ� ���t�F11��18��(��) 0��37�� | |||||||||||||
|
|
|||||
| ���O�F�����E ���t�F11��17��(��) 21��32�� | |||||
|
|
|||||||||
| ���O�Fkoh ���t�F11��17��(��) 19��51�� | |||||||||
|
|
|||||
| ���O�F���C�_�[ ���t�F11��16��(��) 22��50�� | |||||
|
|
|||||
| ���O�F���C�_�[ ���t�F11��16��(��) 22��39�� | |||||
|
|
||
| ���O�F���C�_�[ ���t�F11��16��(��) 22��28�� | ||
|
|
|||||
| ���O�F�R�p�� ���t�F11��16��(��) 20��39�� | |||||
|
|
|||||||||
| ���O�F�W�I�o���j ���t�F11��16��(��) 18��22�� | |||||||||
|
|
|||||
| ���O�F�����i���U�j ���t�F11��16��(��) 16��58�� | |||||
|
|
|||||
| ���O�Ftomtom ���R ���t�F11��16��(��) 16��15�� | |||||
|
|
|||||
| ���O�F���ˁ@���Q ���t�F11��16��(��) 3��24�� | |||||
|
|
|||||
| ���O�F���O�ł��B ���t�F11��15��(��) 23��35�� | |||||
|
|
|||||
| ���O�F���Z3�N���I�I ���t�F11��15��(��) 11��24�� | |||||
|
|
|||||||||
| ���O�F�� ���t�F11��14��(��) 20��56�� | |||||||||
|
|
|||||
| ���O�Frui ���t�F11��14��(��) 13��50�� | |||||
|
|
||
| ���O�F�J�C�g ���t�F11��14��(��) 1��25�� | ||
|
|
|||||||||||||
| ���O�F�Ђ� ���t�F11��14��(��) 0��27�� | |||||||||||||
|
|
|||||||||||||
| ���O�Fyuki ���t�F11��13��(��) 17��50�� | |||||||||||||
|
|
|||||||||||||||||||||||||||||
| ���O�F���C�_�[ ���t�F11��13��(��) 13��33�� | |||||||||||||||||||||||||||||
|
|
|||||||||
| ���O�F�f�U�[�^�[ ���t�F11��13��(��) 12��17�� | |||||||||
|
|
|||||
| ���O�F7777 ���t�F11��13��(��) 11��3�� | |||||
|
|
|||||||||||||||||||||||||
| ���O�F����i���R�j ���t�F11��12��(�y) 21��4�� | |||||||||||||||||||||||||
|
|
|||||||||||||
| ���O�F����i���R�j ���t�F11��12��(�y) 20��57�� | |||||||||||||
|
|
|||||
| ���O�Fhide ���t�F11��12��(�y) 0��15�� | |||||
|
|
|||||||||||||
| ���O�Fren ���t�F11��12��(�y) 0��7�� | |||||||||||||
|
|
|||||||||
| ���O�F�݂�I ���t�F11��11��(��) 21��45�� | |||||||||
|
|
|||||||||||||||||||||||||
| ���O�F���� ���t�F11��11��(��) 17��0�� | |||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
| ���O�F�s�r�h ���t�F11��10��(��) 18��44�� | |||||||||||||||||||||||||||||
|
|
|||||||||||||||||
| ���O�F���w�܂ɂ� ���t�F11��10��(��) 10��49�� | |||||||||||||||||
|
|
|||||||||
| ���O�F���w�܂ɂ� ���t�F11��10��(��) 0��9�� | |||||||||
|
|
|||||||||||||||||
| ���O�F7777 ���t�F11��9��(��) 23��34�� | |||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||
| ���O�F�s�^�S���X ���t�F11��9��(��) 21��41�� | |||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
| ���O�Fcalamity ���t�F11��9��(��) 21��7�� | |||||||||||||||||||||||||||||
|
|
|||||||||
| ���O�Frui ���t�F11��9��(��) 16��34�� | |||||||||
|
|
|||||||||
| ���O�F��o ���t�F11��9��(��) 12��57�� | |||||||||
|
|
|||||||||||||||||
| ���O�F��@��3 ���t�F11��8��(��) 22��25�� | |||||||||||||||||
|
|
|||||||||
| ���O�F���� ���t�F11��8��(��) 20��20�� | |||||||||
|
|
|||||||||||||||||||||
| ���O�F����i��3�j ���t�F11��8��(��) 19��54�� | |||||||||||||||||||||
|
|
|||||||||||||||||
| ���O�F����� ���t�F11��8��(��) 18��22�� | |||||||||||||||||
|
|
|||||||||||||||||
| ���O�F�� ���t�F11��7��(��) 21��31�� | |||||||||||||||||
|
|
|||||
| ���O�F�N�[�f�^ ���t�F11��7��(��) 19��41�� | |||||
|
|
|||||||||||||||||||||||||||||||||||||
| ���O�F����� ���t�F11��7��(��) 18��14�� | |||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||
| ���O�Foh ���t�F11��7��(��) 13��34�� | |||||||||||||||||||||
|
|
|||||
| ���O�F���V�@���j ���t�F11��6��(��) 22��35�� | |||||
|
|
|||||||||||||||||
| ���O�F�f�U�[�^�[ ���t�F11��6��(��) 12��20�� | |||||||||||||||||
|
|
|||||
| ���O�F�߂��i���R�j ���t�F11��6��(��) 11��40�� | |||||
|
|
|||||||||
| ���O�F���[�� ���t�F11��6��(��) 0��33�� | |||||||||
|
|
|||||||||||||||||
| ���O�F���� ���t�F11��5��(�y) 22��18�� | |||||||||||||||||
|
|
|||||||||||||||||
| ���O�F����i���R�j ���t�F11��4��(��) 23��55�� | |||||||||||||||||
|
|
|||||||||||||
| ���O�F���� ���t�F11��4��(��) 21��55�� | |||||||||||||
|
|
|||||
| ���O�F�g�b�V�� ���t�F11��4��(��) 20��19�� | |||||
|
|
|||||
| ���O�F�����鏬�� ���t�F11��3��(��) 23��21�� | |||||
|
|
|||||||||||||
| ���O�F�t ���t�F11��3��(��) 22��33�� | |||||||||||||
|
|
|||||||||
| ���O�F��w���i��3�j ���t�F11��2��(��) 22��30�� | |||||||||
|
|
|||||||||
| ���O�F����i���R�j ���t�F11��2��(��) 18��29�� | |||||||||
|
|
|||||
| ���O�Fmae ���t�F11��2��(��) 10��47�� | |||||
|
|
|||||||||||||
| ���O�F�ցi����j ���t�F11��1��(��) 22��39�� | |||||||||||||
|
|
|||||||||
| ���O�F�Ђ� ���t�F11��1��(��) 22��29�� | |||||||||
|
|
|||||
| ���O�F�p�b�N�� ���t�F11��1��(��) 22��6�� | |||||
|