１から１００までの自然数の和

問題　　　1+2+3+4+････････+98+99+100 = 5050 の計算を、順々に足していく方法より、楽にできる
　　　　方法をできるだけ多く見つけなさい。
　　　　ただし、単に公式を使って　１００×１０１÷２＝５０５０　とする方法は省きます。
　　　　また、以下の計算の答えは、既に分かっているものとして使用しても構いません。
　　　　　1 + 2 = 3
　　　　　1 + 2 + 3 = 6
　　　　　1 + 2 + 3 + 4 = 10
　　　　　1 + 2 + 3 + 4 + 5 = 15
　　　　　1 + 2 + 3 + 4 + 5 + 6 = 21
　　　　　1 + 2 + 3 + 4 + 5 + 6 + 7 = 28
　　　　　1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 = 36
　　　　　1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 = 45
　　　　　1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10 = 55

ヒント　　足す順序を変える、正方形に並べてみる、図で表す、など。

1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100


解法１
　　　　1+2+3+･････････+98+99+100 の順序を逆にした式を元の式の下に書き、
　　　　上下同じ位置の数どうしを足す。

1+ 2+ 3+ ・・・・・・ 98+ 99+ 100
+ 100+ 99+ 98+ ・・・・・・ 3+ 2+ 1
101+ 101+ 101+ ・・・・・・ 101+ 101+ 101 =101×100＝10100

　　　　この 10100 は、1+2+3+･････････+98+99+100 を２回足したものなので、２で割って、
　　　　　　　1+2+3+･････････+98+99+100 = 10100 ÷ 2 = 5050


解法２（解法１の変形）
　　　　　1+2+3+･････････+98+99+100 を 50 のところで折り返して２段に書き、上下を足す。

1+ 2+ 3+ ・・・・・・ 48+ 49+ 50
+ 100+ 99+ 98+ ・・・・・・ 53+ 52+ 51
101+ 101+ 101+ ・・・・・・ 101+ 101+ 101 =101×50＝5050


解法３（解法２の別表現）
　　　　　1+2+3+･････････+98+99+100 の足す順序を変えて
　　　　　 (1+100)+(2+99)+(3+98)+･･･････････････+(48+53)+(49+52)+(50+51) = 101×50 = 5050


解法４（解法１の図形表現）
　　　　下のような三角形のマス目を数えると考え、同じ図形を２つ付けて長方形にする。


　　　　長方形のマス目数は　100×101=10100
　　　　三角形はその半分で　10100÷2=5050


解法５（解法２の図形表現）

　　　　マス目数は　50×101 = 5050



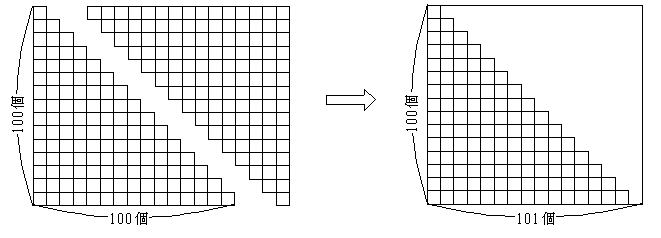
解法６（面積としての計算）

　　　　大きい三角形の面積＝100×100÷2=5000
　　　　小さい三角形の面積＝1×1÷2=0.5
　　　　それが100個あるから　0.5×100=50 　　　　合計　　5000+50=5050


解法７（正方形に並べ横に足す）
　　　　例えば、11+12+1314+15+16+17+18+19+20 は、 1+2+3+4+5+6+7+8+9+10 より各項が 10 ずつ多
　　　　いので、合計では 100 多くなることを利用して２行目以降は計算する。

1+ 2+ 3+ 4+ 5+ 6+ 7+ 8+ 9+ 10= 55
11+ 12+ 13+ 14+ 15+ 16+ 17+ 18+ 19+ 20= 155
21+ 22+ 23+ 24+ 25+ 26+ 27+ 28+ 29+ 30= 255
31+ 32+ 33+ 34+ 35+ 36+ 37+ 38+ 39+ 40= 355
41+ 42+ 43+ 44+ 45+ 46+ 47+ 48+ 49+ 50= 455
51+ 52+ 53+ 54+ 55+ 56+ 57+ 58+ 59+ 60= 555
61+ 62+ 63+ 64+ 65+ 66+ 67+ 68+ 69+ 70= 655
71+ 72+ 73+ 74+ 75+ 76+ 77+ 78+ 79+ 80= 755
81+ 82+ 83+ 84+ 85+ 86+ 87+ 88+ 89+ 90= 855
91+ 92+ 93+ 94+ 95+ 96+ 97+ 98+ 99+ 100= 955
5050

解法８（解法７の発展形）　合計の出し方に工夫する。

1+ 2+ 3+ 4+ 5+ 6+ 7+ 8+ 9+ 10= 55
11+ 12+ 13+ 14+ 15+ 16+ 17+ 18+ 19+ 20= 100+55
21+ 22+ 23+ 24+ 25+ 26+ 27+ 28+ 29+ 30= 200+55
31+ 32+ 33+ 34+ 35+ 36+ 37+ 38+ 39+ 40= 300+55
41+ 42+ 43+ 44+ 45+ 46+ 47+ 48+ 49+ 50= 400+55
51+ 52+ 53+ 54+ 55+ 56+ 57+ 58+ 59+ 60= 500+55
61+ 62+ 63+ 64+ 65+ 66+ 67+ 68+ 69+ 70= 600+55
71+ 72+ 73+ 74+ 75+ 76+ 77+ 78+ 79+ 80= 700+55
81+ 82+ 83+ 84+ 85+ 86+ 87+ 88+ 89+ 90= 800+55
91+ 92+ 93+ 94+ 95+ 96+ 97+ 98+ 99+ 100= 900+55
4500+550 =5050


解法９（正方形に並べ縦に足す）
　　　1+11+21+31+41+51+61+71+81+91 = (10+20+30+40+50+60+70+80+90)+1×10 = 450+10 = 460 のように計算する。

1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90
+91 +92 +93 +94 +95 +96 +97 +98 +99 +100
460 +470 +480 +490 +500 +510 +520 +530 +540 +550 =5050


解法１０（解法９の発展形）
　　　 460+470+480+490+500+510+520+530+540+550 =(450+10)+(450+20)+(450+30)+････････+(450+100)
　　= 450×10 + (10+20+30+40+50+60+70+80+90+100) = 4500 + 550 = 5050


解法１１

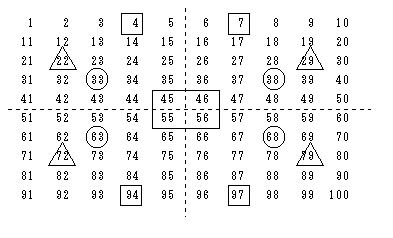
　　　　上図で、正方形の中心軸に対して互いに対称な位置にある４つの数の和はいずれも 202 とな
　　　る。上図の例では、( 4, 7,94,97),(22,29,72,79),(33,38,63,68),(45,46,55,56)。
　　　　このような組が 25 あるので、
　　　　　　　　　　202×25 = 5050


解法１２

　　　　上図で、線で区切られた１０個ずつの数の和はいずれも505であるから、
　　　　　 505×10=5050


解法１３（解法１２の別表現）

1 2 3 4 5 6 7 8 9 10
12 13 14 15 16 17 18 19 20 | 11
23 24 25 26 27 28 29 30 | 21 22
34 35 36 37 38 39 40 | 31 32 33
45 46 47 48 49 50 | 41 42 43 44
56 57 58 59 60 | 51 52 53 54 55
67 68 69 70 | 61 62 63 64 65 66
78 79 80 | 71 72 73 74 75 76 77
89 90 | 81 82 83 84 85 86 87 88
+100 | +91 +92 +93 +94 +95 +96 +97 +98 +99
505 +505 +505 +505 +505 +505 +505 +505 +505 +505 =5050

　　　上のように、正方形に数字を並べる。 ある列と、その左の列とでは、｜で仕切られた部分は、左の数の方が９大きく、
　　その他の９カ 所は１ずつ小さいので、左右の列の合計は同じとなる。


解法１４（各位の数に分けて足す）
　　　　１の位の数は、０〜９が１０組あるので、４５×１０＝４５０
　　　　１０の位の数は、００〜９０が１０組あるので、４５０×１０＝４５００
　　　　１００の位は１００だけ。
　　　　従って、 　　450+4500+100=5050


「算数・数学」の部屋に戻る