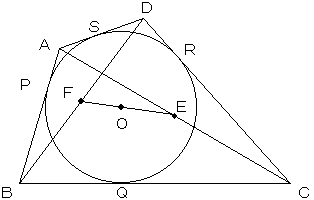
円に外接する四角形の2本の対角線の中点と、円の中心は同一直線上にある。
ニュートンの定理1

円に外接する四角形の2本の対角線の中点と、円の中心は同一直線上にある。
予備証明
△ADOと△BCOが、点Oを共有して、互いに、重ならずに存在するとします。
このとき、点Lを
△ADO+△BCO=△ADL+△BCL
となるようにとるとき、点Lは、点Oを含む直線上にある。
ADとBCが平行なときは、点Oを通って、ADに平行な直線が、点Lの存在する
範囲であることは明らかであるので、ADとBCが平行でない場合を考えます。
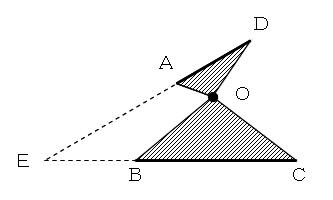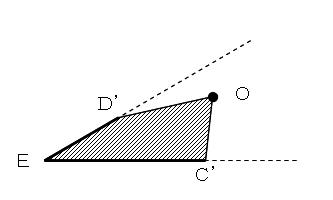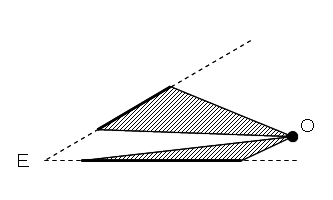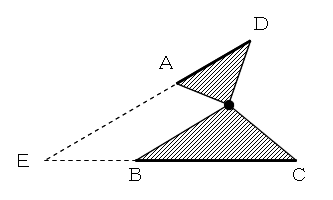
ADとBCの交点をEとし、線分AD,BCを一方の端点が、点Eに重なるまで、等積変形します。
このとき、線分AD,BCがそれぞれ、線分ED’,EC’に移動したとします。
四角形D’EC’Oは、△ADO+△BCO を保持しています。
ここで、点Oを通り、D’C’に平行な直線を引き、この直線上に点Oとは違う点Lをとると、
四角形D’EC’Lは、四角形D’EC’Oと面積は等しく、△ADO+△BCO を保持しています。
さらに、線分ED’,EC’を元の線分AD,BCの位置まで等積変形すると、
△ADL+△BCL は、△ADO+△BCO を保持しています。
よって、条件を満たす点Lは、点Oを含む直線上にあります。
ただし、その直線は、直線ADや、直線BCを越えないこととします。
証明
EはACの中点なので、
△ABE=△ABC / 2
△CDE=△ACD / 2
2式を足して
△ABE+△CDE=四角形ABCD / 2 ………(1)
同様に
△ABF+△CDF=四角形ABCD / 2 ………(2)
また、四角形ABCDは円Oに外接するのだから、辺AB,BC,CD,DA上の円との接点をそれぞれP,
Q,R,Sとすると、
AS=AP,BP=BQ,CQ=CR,DR=DS
これより、
AB+CD=AD+BC
円の半径をrとすると、
△ABO=r・AB/2,△CDO=r・CD
/ 2
これより
△ABO+△CDO=r・(AB+CD) /
2
同様に
△ADO+△BCO=r・(AD+BC) /
2
ゆえに
△ABO+△CDO=△ADO+△BCO
この両辺の和は四角形ABCDの面積に等しいので、
△ABO+△CDO=四角形ABCD / 2 ………(3)
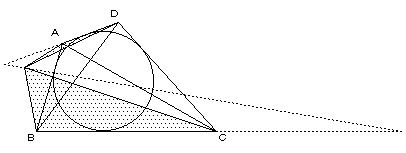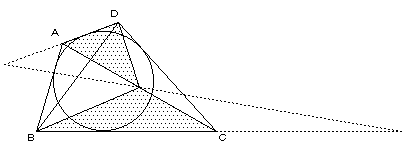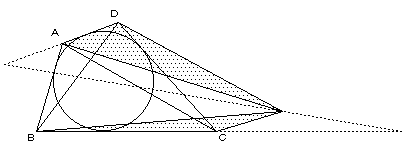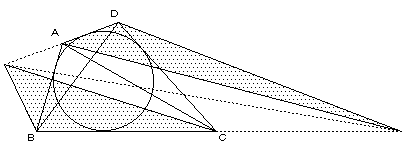
△ABL+△CDL=(一定)であるような点 L は一直線上にある(予備証明より)ので、
(1),(2),(3)より、3点E,F,O は、一直線上にある。
証明終わり
special thanks bunny_star さん