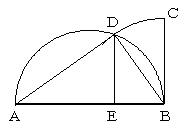
ABを1辺とする正方形を3つ図のように描き
Aから対角線ACを引き、ABを含む正方形との
交点をDとし、DからABに下ろした垂線の足Eが
3等分点のひとつとなります。
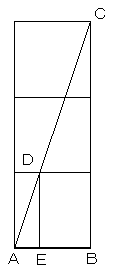
ABを1辺とする正方形を6つ図のように描き
Aから対角線ACを引き、ABを含む正方形との
交点をDとし、DからABに下ろした垂線の足Eが
3等分点のひとつとなります。
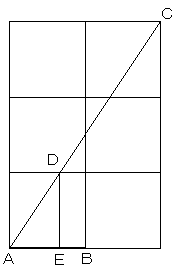
ABを1辺とする正方形を3つ図のように描き
対角線CDと、ABの交点Eが3等分点のひとつ
になります。

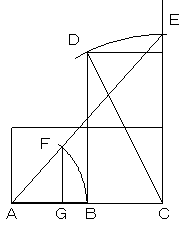
ABを1辺とする正方形を図のように4つ描き、
長さBCをBDの延長上に取り、AEを結びます。
AB=AFとなる点FをAE上にとり、点FからABに
下ろした垂線の足Gが3等分点のひとつになります。
(説明)
ABを1とすると、BCは2√2となります。
△ABEにおける三平方の定理より、AE=3となります。
この上に長さ1のAFを取ることにより、1/3 の長さを作っています。
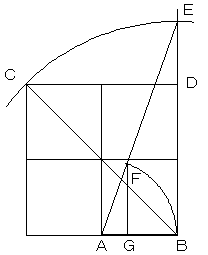
ABを1辺とする正方形を図のように3つ描き、
長さCDをCEに取り、AEを結びます。
AB=AFとなる点FをAE上にとり、点FからABに
下ろした垂線の足Gが3等分点のひとつになります。
(説明)
ABを1とすると、CDは√5 となります。
△ACEにおける三平方の定理より、AE=3となります。
この上に長さ1のAFを取ることにより、2/3 の長さを作っています。
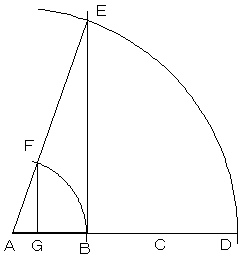
ABをB方向に2倍伸ばした点Dを取ります。
中心A、半径ADの円と、BからABに垂直に
延ばした直線との交点をEとし、AEを結びます。
AB=AFとなる点FをAE上にとり、点FからABに
下ろした垂線の足Gが3等分点のひとつになります。
方法4の辺の取り方の変更です。
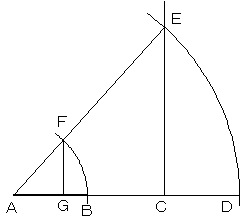
ABのBの方向に点C点DをAB=BC=CDとなるように取ります。
中心A、半径ADの円と、CからABに垂直に
延ばした直線との交点をEとし、AEを結びます。
AB=AFとなる点FをAE上にとり、点FからABに
下ろした垂線の足Gが3等分点のひとつになります。
方法4の辺の取り方の変更です。
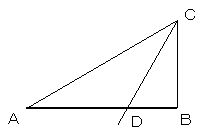
ABの両端が、30°、90°の直角三角形ABCを描くと、∠ACBの
二等分線とABの交点Dが、3等分点のひとつになります。
(説明)
△ABC、△CBDはともに、30°を含む直角三角形です。
DB=1とすると、BC=√3、AB=3となり、点Dは、ABの
3等分点になっています。
ABの両端が、30°、90°の直角三角形ABCを描くと、斜辺ACの
垂直二等分線と、ABの交点Eが、3等分点のひとつになります。
(説明)
△ABC、△ADEはともに、30°を含む直角三角形です。
BC=1とすると、AB=√3。
一方、AC=2よりAD=1であり、AE=2/√3=2√3/3
よって、AE=(2/3)AB となり、点EはABの3等分点になっています。
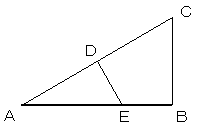
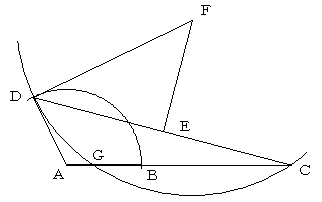
AB:AC=√3:1 の長さの線分ACを取り、ABと適当
な角度で配置します。
点Cから引いたACの垂線と、CBの垂直二等分線の交点
をEとし、中心E、半径CEの円と、ABの交点FがABの
3等分点のひとつになります。
(説明)
AB=3とすると、AC=√3
方べきの定理より、
AC2=AF・AB
√32=3AF
よって、AF=1 となり、点Fは、ABの3等分点になっています。
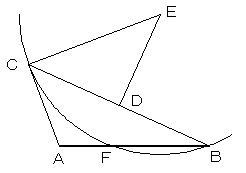
点AからABの方向以外に半直線を引き、AC=CD=DE
となる点C,D,Eをこの順に取ります。
点Cを通って、BEに平行な直線とABとの交点Fが、3等分点
のひとつになります。
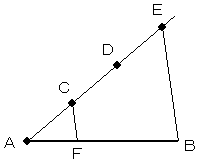
方法11と同じように、点C、D、Eを取り、BEを結びます。
BEの中点と点Aを結んだ線と、BCの交点をFとします。
EFの延長と、ABの交点Gが、3等分点のひとつとなります。
(説明)
チェバの定理を使っています。
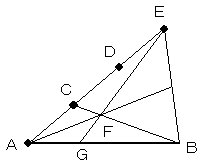
ABと同方向でない、適当な線分ACをとり、ACの中点Dと
Bを結びます。BDの中点をEとし、CEとABの交点Fが、
3等分点のひとつとなります。
(説明)
メネラウスの定理を使っています。
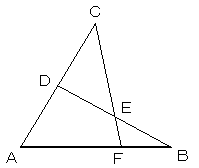
Aを通り、ABと同方向でない直線を引き、この直線上に
AC=ADとなる2点C、Dを、点Aをはさんで両側に取ります。
CBの中点をEとし、DEとABの交点Fが、ABの3等分点のひとつになります。
(説明)
メネラウスの定理を使っています。
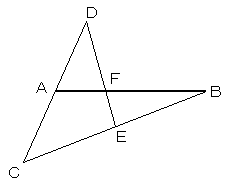
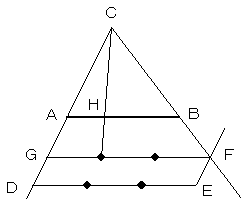
ABとは同一直線上にない点Cをとり、Cから出る
半直線CA,CBを引きます。
CA上のある点DからABに平行に線分DEを引きます。
Dから、その直線上に等間隔に3つ点を取り、
3つめを点Eとします。
点EからCAに平行に引いた直線と、CBの交点を
Fとし、点Fを通って、ABに平行な直線とCAとの
交点をGとすると、FGはDEと同じ長さになります。
FGの三等分点のひとつと点Cを結び、ABとの交点Hが、
三等分点のひとつとなります。
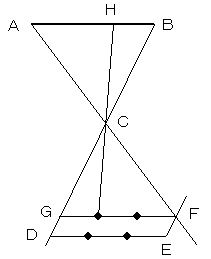
方法15で、半直線CA,CBをAおよびBから
出した場合です。
AC=3AB となる点Cを、直線AB上のB側に取ります。
AB=ADとなる線分ADを、ABとは違う方向に取ります。
点DからADに垂直に引いた直線と、CDの垂直二等分線
との交点をFとし、中心F、半径FDの円と、ABとの
交点Gが、三等分点のひとつになります。
(説明)
AB=AD=3 とおくと、AC=9
方べきの定理より、
AD2=AG・AC
9=9AG
AG=1
となり、GはABの三等分点のひとつとなります。
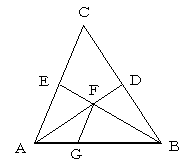
ABを1辺に持つ、適当な三角形ABCを作り、
BCの中点をD、ACの中点をEとし、ADとBEの
交点をFとします。(Fは△ABCの重心です)
点Fから、ACに平行に引いた直線とABとの交点Gが、
ABの三等分点のひとつになります。
Aを中心に適当な半径の円を描き、Bを中心に
その2倍の半径の円を描き、交点をEとします。
∠AEBの二等分線とABとの交点Fが、ABの三等分点のひとつになります。
(説明)
角の二等分線の定理より、
AF:FB=AE:EB=1:2
となります。
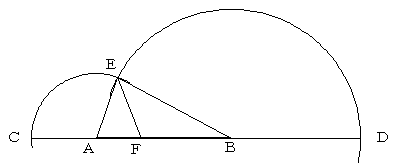
AB=BCとなる点CをABのB側の延長上に取ります。
点A中心、半径ABの円と、点B中心、半径ABの半分の円との
交点をDとします。
(AD:DB=2:1 になれば、どんな長さでも良いです)
CDの垂直二等分線と、BCの交点をFとし、
点F中心、半径FCの円とABの交点をGとすると、
点GはABの三等分点のひとつになります。
(説明)
アポロニウスの定理より、
AG:GB=AC:CB=2:1
になります。
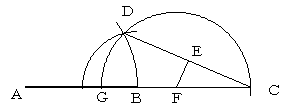
AB:BC=√3:1 となる線分BCを引きます。
点B中心、半径BCの円と、ABを直径とする円との交点を
Dとし、DからABに下ろした視線の足Eが、
ABの三等分点のひとつになります。
(説明)
△ABDは∠ADB=90°の直角三角形になります。
AB=√3 とすると、BD=1。
△ABDにおける三平方の定理より、
AD=√2
△DBE,△ADEは△ABDと相似な三角形なので、
BE:ED=ED:AE=1:√2
よって、
BE:AE=1:2
となります。