定理
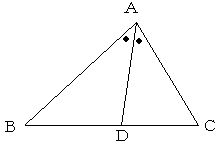
△ABCにおいて、∠Aの2等分線とBCの交点をDとするとき
BD:DC=AB:AC
が成り立つ。
証明
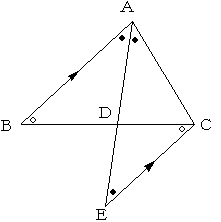
点Cを通り、ABに平行な直線と、ADの交点をEとします。
このとき、
∠BAE=∠CEA (錯角)
より、
∠CEA=∠CAE(=∠BAE)
となり、△ACEは、AC=CE の二等辺三角形となります。
一方、△ABDと△ECDが相似であることより
BD:DC=AB:CE
よって、AC=CE より、
BD:DC=AB:AC
が成り立ちます。
算数・数学の部屋に戻る
角の2等分線の定理
定理

△ABCにおいて、∠Aの2等分線とBCの交点をDとするとき
BD:DC=AB:AC
が成り立つ。
証明

点Cを通り、ABに平行な直線と、ADの交点をEとします。
このとき、
∠BAE=∠CEA (錯角)
より、
∠CEA=∠CAE(=∠BAE)
となり、△ACEは、AC=CE の二等辺三角形となります。
一方、△ABDと△ECDが相似であることより
BD:DC=AB:CE
よって、AC=CE より、
BD:DC=AB:AC
が成り立ちます。
算数・数学の部屋に戻る