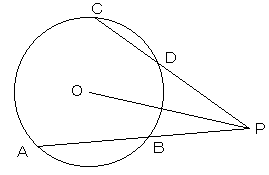
円外の点Pから円に交わる2本の直線を引くとき、
以下の等式が成り立つ。
AP・BP=CP・DP=OP2−r2 (r は円の半径)
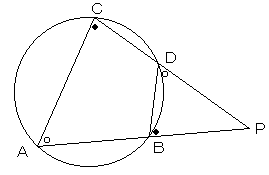
△ACPと△DBPにおいて、
円に内接する四角形のある角と、向かい合う角の外角
が等しいことより、
∠CAP=∠BDP、∠ACP=∠DBP
以上より、△ACPと△DBPは相似。
よって、
AP:CP=DP:BP
AP・BP=CP・DP
(=OP2−r2 の証明は、ii) で併せて証明)
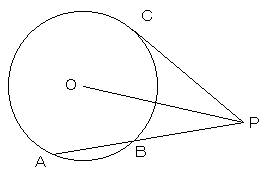
円外の点Pから円に交わる直線および接線を引くとき、
以下の等式が成り立つ。
AP・BP=CP2=OP2−r2 (r は円の半径)
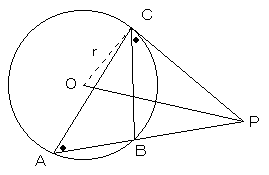
△ACPと△CBPにおいて、接弦定理より
∠CAP=∠BCP
また、
∠CPA=∠BPC(共通)
以上より、△ACPと△CBPは相似。
よって、
AP:CP=CP:BP
AP・BP=CP2
また、△OCPにおいて、
∠OCP=∠R
より、
CP2=OP2−r2
よって、i) の場合もあわせて、
AP・BP=OP2−r2
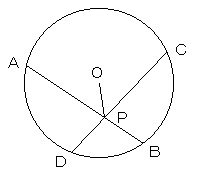
円内の点Pから2本の直線を引くとき、以下の等式が成り立つ。
AP・BP=CP・DP=r2−OP2
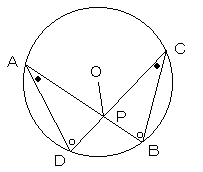
△ADOと△CBOにおいて、
∠DAO=∠BCO
∠ADO=∠CBO (いずれも同一弦に立つ円周角)
より、△ADOと△CBOは相似。
よって、
AP:DP=CP:BP
AP・BP=CP・DP
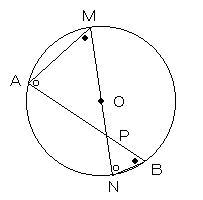
また、図のように、2点O、Pを通る直径MNを引く。
既に証明した方べきの定理より、
AP・BP=MP・NP
ここで
MP=r+OP、NP=r−OP
より、
AP・BP=r2−OP2