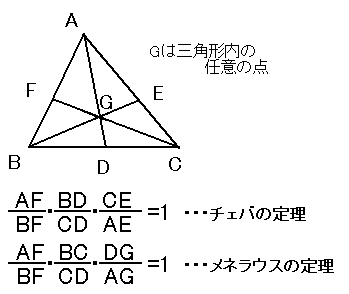
チェバの定理の証明
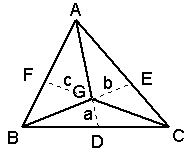
図のように、a=△BCG、b=△CAG、c=△ABG とします。
AF/BF=b/a、BD/CD=c/b、CE/AE=a/c
より、
(AF/BF)(BD/CD)(CE/AE)=(b/a)(c/b)(a/c)=1
メネラウスの定理の証明
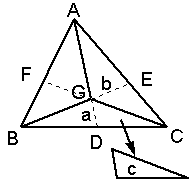
図のように、a=△BCG、b=△CAG、c=△DCG とします。
AF/BF=b/a、BC/CD=a/c、DG/AG=c/b
より、
(AF/BF)(BC/CD)(DG/AG)=(b/a)(a/c)(c/b)=1
チェバの定理の拡張形
点Gが△ABCの外にあるときも、成り立ちます。
証明1(点Gが三角形の外角の範囲内にあるとき)
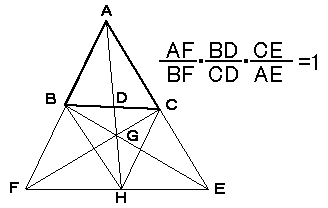
EFとADの交点をHとすると、チェバの定理(基本形)より、
(AB/BF)(FH/HE)(EC/CA)=1
これを三角形の面積比で表すと、
(△ABH/△BFH)(△AFH/△AEH)(△ECH/△CAH)=1
順番を組み替えて
(△AFH/△BFH)(△ABH/△CAH)(△ECH/△AEH)=1
それぞれ、底辺比に置き換えると、
(AF/BF)(BD/CD)(CE/AE)=1
となり、チェバの定理(拡張形)が証明された。
証明2(点Gが三角形の内角の対頂角の範囲内にあるとき)
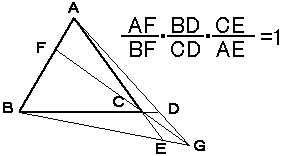
辺の比を、三角形の面積比で表すと、
AF/BF=△ACG/△BCG
BD/CD=△ABG/△ACG
CE/AE=△BCG/△ABG
以上より、
(AF/BF)(BD/CD)(CE/AE)=1
「算数・数学の部屋」に戻る