実数 a、b および、虚数単位 i に対し
z=a+bi
で表される数を複素数といいます。 参照
a を実部、b を虚部といいますが、実部をx軸、虚部をy軸に取り
座標平面上で複素数を表したものを複素数平面といいます。
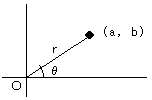
図のように、点 (a, b) が a+bi を表します。
このとき、原点から点 (a, b) 距離までの距離を r、ベクトル (a, b) のx 軸からの回転角を θ と
すると、z=a+bi は、
z=r(cosθ+isinθ)
と書けます。
r をこの複素数の絶対値、θを偏角といいます。ただし、ここでは簡単のため、r を長さと呼ぶことにします。
オイラーの公式により、
z=reiθ
と書くと、複素数どうしの掛け算、割り算、べき乗などを容易に計算できます。
実数 a,b,c,d に対し、
x=a+bi=reiθ
y=c+di=seiφ
の2つの複素数を決めます。これらについて各種演算を以下のように決めることが出来ます。
加減算
x±y=(a±c)+(b±d)i (複合同順)
2つのベクトル (a, b), (c, d) の和、差として表せます。
積
xy=reiθ×seiφ=rsei(θ+φ)=rs{cos(θ+φ)+isin(θ+φ)}
xy は xの長さをs倍し、φだけ回転したものになります。
これを、 e を使わずに計算すると以下のようになります。
xy=r(cosθ+isinθ)×s(cosφ+isinφ)
=rs{(cosθcosφ−sinθsinφ)+(sinθcosφ+cosθsinφ)i}
=rs{cos(θ+φ)+isin(θ+φ)}
商
y≠0のときにおいて、
x/y=reiθ/seiφ=(r/s)ei(θ−φ)=(r/s){cos(θ−φ)+isin(θ−φ)}
x/y は、xの長さを 1/s 倍し、−φだけ回転したものになります。
実数乗
実数mに対して
xm=(reiθ)m=rmeimθ=rm{cos(mθ)+isin(mθ)}
xmは x の長さを m乗、回転角をm倍したものになります。
累乗根
実数乗において、m=1/nとおいた
x1/n=(reiθ)1/n=n√reiθ/n=n√r{cos(θ/n)+isin(θ/n)}
も、累乗根の1つではありますが、すべてではありません。
複素数の範囲では、n乗根はn個あります。つまり、
長さに関しては、n乗して r になる実数は n√r ですが、
n倍してθになる角度は、θ+2π、θ+4π なども同じ角度であることを考慮すると、
(θ+2kπ)/n (k=0, 1, ・・・,n-1)
と書けます。つまり、θ/n から 2π/n ずつ刻んだn個の角度ということになります。
例えば、1の3乗根、4乗根、5乗根は下図の通りです。
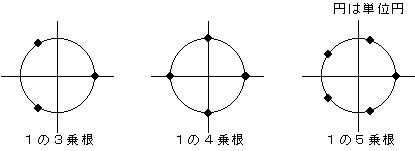
余談ですが、この方法で、−1×(−1)=1 を説明することができます。
まとめると、x の n乗根は、
n√r・e(θ+2kπ)i/n (k=0, 1, ・・・,n-1)
と表せます。
eの複素数乗
ex=ea+bi=eaebi=ea(cosb+isinb)
実数の複素数乗
実数mは
m=elogm (log は自然対数) と書けるので、
mx=ma+bi=mambi=ma(elogm)bi=maebi・logm
=ma{cos(b・logm)+isin(b・logm)}
複素数の複素数乗
xy=(reiθ)y=ryeiθ(c+di)=rye(-dθ+icθ)=rcedi・logre(-dθ+icθ)
=rce-dθei(d・logr+cθ)=rce-dθ{cos(d・logr+cθ)+isin(d・logr+cθ)}
「算数・数学」の部屋に戻る