柴田さんからの質問1
質問
幾何学でベクトルが役に立つとよく言うんですが、
普通の図形の問題などでは、どう利用したらいいのか分かりません。
ベクトルではない線分とかってベクトル成分とかで表せないんですか?
回答(以下太線はベクトルを表します)
ベクトルの基本的なことは、こちらやこちらを見ていただくとして、
例として、三角形の重心が、中線を2:1に内分する点であることを
ベクトルを使って示します。
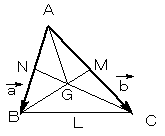
△ABCにおいて、BC,CA,ABの中点をL,M,N
とします。
a=AB, b=AC
とおき、AGをaとbで表すことを考えます。
その結果、AG=2AL/3、BG=2BM/3、CG=2CN/3 が言えることを示します。
使用する基本性質1
2点B、Cについて、a=AB、b=ACとするとき
BC=b−a
で表される。 |
使用する基本性質2−1
2点B、Cについて、a=AB、b=ACとするとき、BCをm:nに内分する点ををPとするとき、
AP=(mb+na)/(m+n) ………(1)
で表せる。
同様に、BCをm:nに外分する点ををPとするとき、
AP=(mb−na)/(m−n) ………(2)
で表せる。 |
使用する基本性質2−2
上記(1) において、t=m/(m+n) とおくと、n/(m+n)=1−t
なので、
AP=tb+(1−t)a
と書ける。ただし、0<t<1
上記(2)において、t=m/(m−n) とおくと、−n/(m−n)=1−t
なので、
AP=tb+(1−t)a
と書ける。ただし、m>nのとき、t>1。m<nのとき、t<0。
また、
AB=0b+(1−0)a
AC=1b+(1−1)a
以上より、直線BC上の任意の点Pについて、
AP=tb+(1−t)a (tは任意の実数)
と書ける。特に、0<t<1 のとき、Pは線分BC上にある。 |
使用する基本性質3
aとbが一次独立(平行でない)のとき、
ma+nb=0 ならば m=0 かつ n=0
拡張して、
ma+nb=pa+qb ならば m=p かつ n=q |
AM=b/2 より、線分BM上の任意の点Pについて、
AP=sAM+(1−s)AB=sb/2+(1−s)a (ただし、0<s<1)
AN=a/2 より、線分CN上の任意の点Qについて、
AQ=tAC+(1−t)AN=tb+(1−t)a/2 (ただし、0<t<1)
が成り立つ。
GはBMとCNの交点なので、
AP=AQ
が成り立つときのs、tの値における、AP,AQがいずれもAGを表す。
AP=AQより、
sb/2+(1−s)a=tb+(1−t)a/2
基本性質3より、
s/2=t かつ 1−s=(1−t)/2
これを解いて、s=2/3、t=1/3。このとき、
AG=a/3+b/3
LはBCの中点なので、
AL=a/2+b/2
よって、AG=2AL/3 ………(a)
BG=AG−AB=a/3+b/3−a=b/3−2a/3
BM=AM−AB=b/2−a
よって、BG=2BM/3 ………(b)
CG=AG−AC=a/3+b/3−b=a/3−2b/3
CN=AN−AC=a/2−b
よって、CG=2CN/3 ………(c)
(a)(b)(c) より、重心は中線を2:1に内分する点であることが言える。
算数・数学の部屋に戻る
