算チャレ過去問補完計画2
算チャレ過去問補完計画1へ
第88回

図のように等積変形すると、面積比は、
BP:(PC+CQ):QD=5:11:8
QD=4cm より、BP=2.5cm
また、BC+CD=(5+11+8)÷2=12cm より
BC=CD=6cm
ここで、5:12:13の直角三角形より、AP=13/2としても良いが、
この比は以下のようにしても求められる。
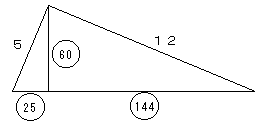
上記の三角形の面積は、 5×12÷2=30
一方、丸数字を使った面積は
(25+144)×60÷2=5070
よって、(1)の2乗は、1/169となる。
(1)=1/13
斜辺は 169×1/13=13
答え 13/2
第90回
こちら参照のこと
第91回
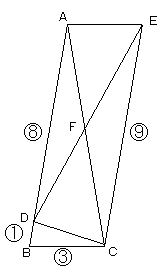
図のように、△ABCと△CAEは合同な三角形になります。
よって、ABとCEは平行です。
よって、AF:FC=8:9
△ADC=△ABC×8/9
△FDC=△ADC×9/17=△ABC×8/9×9/17
=△ABC×8/17
答え 8/17倍
第92回
みんなで、75回の支払いが行われました。
1回目から10回目までを調べると、
1,2,4,7,1,6,2,9,7,6 で、1が2回、2が2回、4が1回、6が2回、7が2回、9が1回です。
さらに20回まで調べます。
11,12 と進めるのは、1,2 と進めるのと同じなので、
11回目から20回目までは、上記の数が5ずつずれて、
6,7,9,2,6,1,7,4,2,1 で、1が2回、2が2回、4が1回、6が2回、7が2回、9が1回
これで1に戻ったので、このあと10回ごとに、同じ数ずつ増えていきます。つまり、
70回目までで、
1が14回、2が14回、4が7回、6が14回、7が14回、9が7回
このあと、6,7,9,2,6
と続くので、6番目のひとが最も多く、16回払った。
答え 1600円
算チャレ過去問補完計画3へ
算数・数学の部屋に戻る


