算チャレ過去問補完計画１

算数にチャレンジ（通称算チャレ）の過去問で、解説がなく、かつ数学の小部屋にもない
問題の解説をしていきます。

（リンクが切れていたらゴメンナサイ）

第４２回

こちらも参照してください。
長針と短針とで合わせて、1440°回るので、その間の時間は
　1440÷(6+0.5)＝2880/13 (分)
この間に回る短針の角度（＝最初の状態での長針と短針の角度）は、
　2880/13 × 0.5 ＝1440/13 (°)
10時を過ぎてこの角度になるまでの時間は、
　(1440/13−60)÷(6-0.5)＝660/13×2/11＝1320/143＝120/13
　120/13＝９＋3/13
　3/13×60＝180/13＝13＋11/13
答え　１０時９分１３と11/13秒

方程式で解くなら、１０時ｘ分と１時ｙ分とおいて、
　6x=30+0.5y　・・・・・・１と２の間の針の位置
　300+0.5x=6y・・・・・・１０と１１の間の針の位置
より、ｘ＝120/13 を得ます。

第４３回

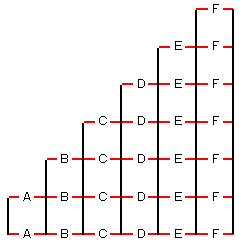
赤は逆戻りできないので、図のアルファベットから、Ａを１つ、Ｂを１つ、・・・Ｆを１つ選んで、
あとはそれらを通るように縦の道を通るようにすればいいので、
　２×３×４×５×６×７＝５０４０（通り）

第４４回
結果から言うと、１７×１８−１７−１８＝２７１　円です。

こちらおよびその解答に解説があります。

第４５回
１個の小さい立方体について、１度に塗られる面は０，１，２，３面です。
よって、塗られている色の数は、色の種類を無視すると、
（０，３，３）（１，２，３）（２，２，２）の３通りです。
・１回目で中心にあって、塗られなかったものは、２回目、３回目で、３面ずつ塗られないといけません。
　２回目、３回目についても同じで、（０，３，３）は３個。
・１回目で面の真ん中にあったもの（１面だけ塗られる）は、２回目、３回目で２面と３面が塗られないといけません。
　それらは２回目、３回目において、互いに重複しないので、（１，２，３）は１８個。
残りが（２，２，２）で、２７−３−１８＝６（個）

第４６回
算チャレVer.3 の第１９問に同じような問題があります。
１つの方法として、

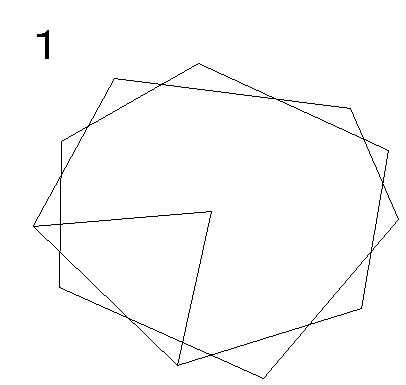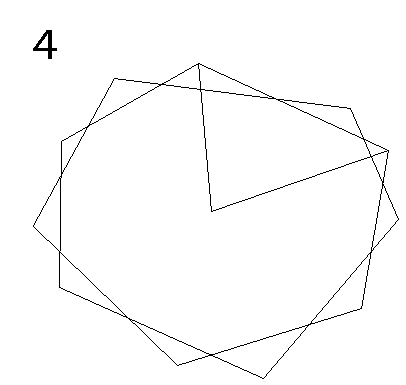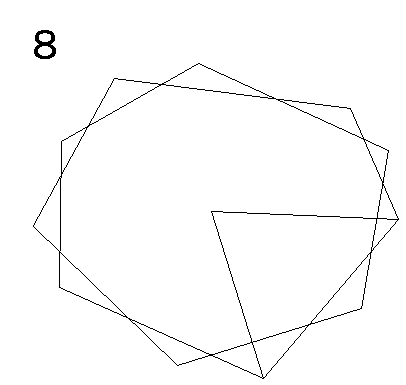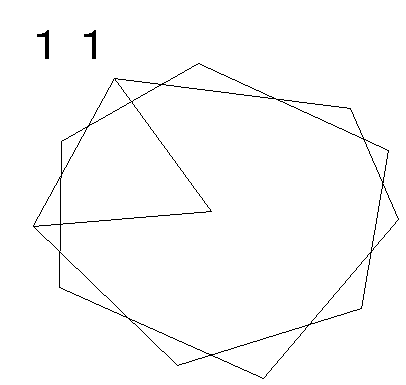
図のように、図形の中ほどに１点を取り、三角形を順に１１個作ります。
三角形の内角の合計は　１８０×１１＝１９８０（°）
このうち、中心付近に２回転分（７２０°）使用しているので、それを引いて、
　１９８０−７２０＝１２６０（°）

第４７回
Ａ、Ｂそれぞれ［１００］とします。Ａの食塩［１２］、Ｂの食塩［０］としても、
一般性を失いません。
合わせて、［１２］の食塩を差が［７］になるようにするには、
［2.5］と［9.5］に分ける。
Ａから、［2.5］の食塩を持ち出す場合
　２００×１２÷２．５＝９６０（ｇ）
Ａから、［9.5］の食塩を持ち出す場合
　２００×１２÷９．５＝4800/19（ｇ）

算チャレ過去問補完計画２へ

算数・数学の部屋に戻る