算チャレ過去問補完計画３

算チャレ過去問補完計画２へ

第９４回

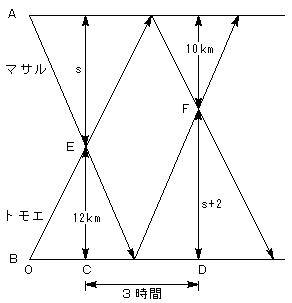
状況をダイヤグラムに描くと上のようになります。
Ａ地点からＥ地点までの距離をｓとすると、Ｆ地点からＢ地点までの距離は、
ｓ＋２となります。
よって、時刻Ｃから時刻Ｄまでの３時間にマサル君の方が４km多く歩いています。
時刻ＣからＤまでの３時間の間に、マサル君、トモエさんの２人でＡＢ間を１往復しています。
時刻０から時刻Ｃまでに、マサル君、トモエさんの２人でＡＢ間の片道を進んでいますので、
時刻０から時刻ＣまではＣＤ間の半分で、１．５時間です。
よって、この間にマサル君の方２km多く歩いているはずです。
よって、ＡＥ間の距離は１４km。
時刻０から時刻Ｃまでの１．５時間の間にマサル君は１４ｋｍ進むので、速度は、
　１４÷１．５＝２８／３
答え　時速２８／３km

第９５回
（途中、単位省略します）

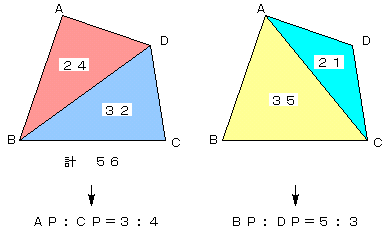
上図左より、四角形ＡＢＣＤの面積が５６であると同時に、
　ＡＰ：ＣＰ＝２４：３２＝３：４
であることがわかります。
上図右より、△ＡＢＣの面積が　５６−２１＝３５　であると同時に
　ＢＰ：ＤＰ＝３５：２１＝５：３
であることがわかります。
以上より、
　△ＡＢＰ＝△ＡＢＤ×5/8＝１５
あるいは、
　△ＡＢＰ＝△ＡＢＣ×3/7＝１５

第９６回

グラフより、ＨＩの長さが40cmであるとわかります。
また、「水の深さの増え方が毎分２cmに変わりました」の記述より、
ＧＨＩＪの面積が　200÷2＝100 cm²であることがわかります。
以上より、求める長さＡＢ（＝ＩＪ）は、
　100÷40＝2.5
答え　2.5cm

第１００回
「マサルさんは４５歩、トモエさんは５４歩歩いたところですれ違いました」
ここまでで、２人は同じ時間同じ距離を歩いているので、
　歩幅の比　マ：ト＝54:45＝６：５
　ペースの比　マ：ト＝５：６
さらに、トモエさんがペースを１．５倍にして７２歩歩いたとき、かかる時間は、元のペースの
　７２÷１．５＝４８歩
と同じです。また、この間に、マサルさんは
　４８×5/6＝４０歩
歩いています。もし、マサルさんが、歩幅を１０cm増加させずに歩いたとすると、
トモエさんがＡ地点に着いたとき、Ｂ地点より、
　８＋４０×0.1＝１２ｍ
手前にいることになります。以上を踏まえて、図を描くと、

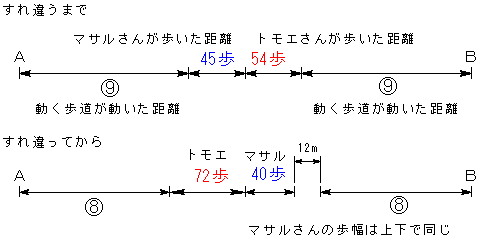
トモエさんについて考えると、
　７２−５４＝１８
１８歩分が、（１）に当たります。（）は○を表します。
よって、すれ違う前で、トモエさんの歩いた距離は、
　５４÷１８＝３
より、トモエさん、マサルさんの歩いた距離は（３）ずつとなり、ＡＢ間の距離は、
　（９）＋（３）＋（３）＋（９）＝（２４）
となります。
一方、マサルさんについて考えると、
　１８×5/6＝15
より、１５歩分が、（１）に当たります。
すれ違ってからの図において、空白の１２ｍは、
　マサルさんの５歩分＋（１）＝（1/3）＋（１）＝（4/3）
に当たります。よって、
　１２÷4/3＝９　より、　（１）＝９ｍとなります。
ＡＢ間の距離は　９×２４＝２１６（ｍ）
トモエさんの歩幅は、　９÷１８＝０．５（ｍ）　５０ｃｍ

第１０１回

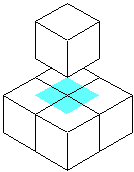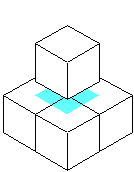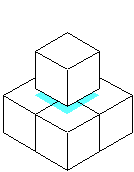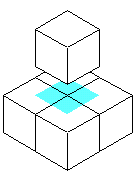
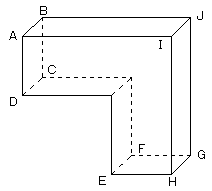
この問題は、「立体を１つ追加しても、表面積が変わらない」状態を見つける問題です。
図のように、１つの立体を追加するときに、１面が接するようにくっつけると、相手方と合わせて、
２面分の面積が減り、都合
　６−２＝４
４面分の面積が増えます。
面積が増えないようにするには、３面が隠れるようにくっつける必要があります。

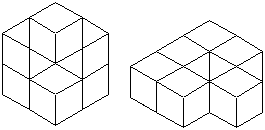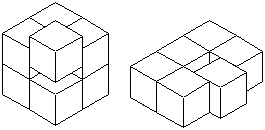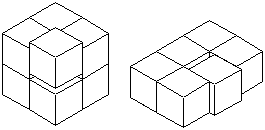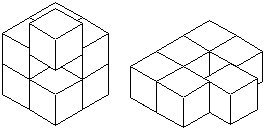
上のような例が考えられますが、個数の少ないのは、
右の方の例で、５個と６個で合わせて、１１個の立体を使っています。

第１０２回
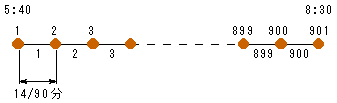
リフトが、下から上まで行くのに
　９００÷９０＝１０
１０分かかります。
５時３０分にリフトに乗った人が、到着点に着くのが５時４０分。
これから、８時３０分までの１４０分間に到着点に着く人数を求めます。
リフトが到着する間隔は、１４÷９０＝14/90 分　（あえて約分しません）
　１４０÷14/90＝900
８時３０分ちょうどに降りた人も数えると、９０１人となります。


算数・数学の部屋に戻る