正１２面体の座標



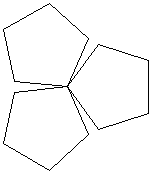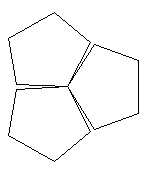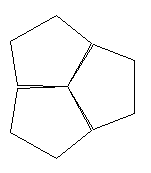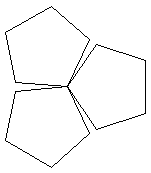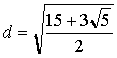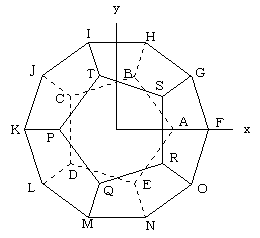
上の図で、正五角形ＡＢＣＤＥはｘｙ平面上にあり、中心が原点と一致しています。
また、点Ａの座標をＡ：（１，０，０）とします。

このとき、点Ｂ，Ｃ，Ｄ，Ｅの座標は、
　Ｂ：（cos72°, sin72°，０）
　Ｃ：（-cos36°, sin36°，０）
　Ｄ：（-cos36°, -sin36°，０）
　Ｅ：（cos72°, -sin72°，０）
となります。　これらの値は、「５倍角の公式」参照。

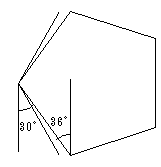
また、「cubeさんからの質問」より、点Ａ、Ｃ、Ｋのｘ座標ｘ_A、ｘ_C、ｘ_Kについて、
　ｘ_A−ｘ_C：ｘ_C−ｘ_K＝√５：１
であるので、
　１＋cos36°＝√５（-cos36°−ｘ_K）
　cos36°＝（√５＋１）／４
より、
　ｘ_K＝−（√５＋１）／２

　Ｘ＝（√５＋１）／２
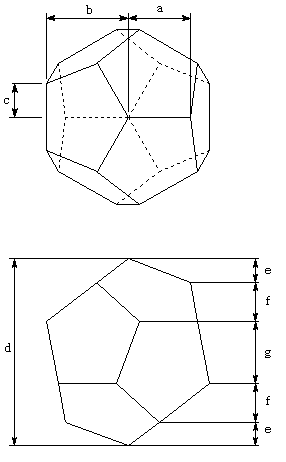
とおくと、「正１２面体の体積」とあわせて、各点の座標が以下のように決まります。
　Ｆ：（Ｘ，０，１）
　Ｈ：（Ｘcos72°，Ｘsin72°，１）
　Ｊ：（-Ｘcos36°, Ｘsin36°，１）
　Ｌ：（-Ｘcos36°, -Ｘsin36°，１）
　Ｎ：（Ｘcos72°, -Ｘsin72°，１）

　Ｇ：（Ｘcos36°, Ｘsin36°，Ｘ）
　Ｉ：（-Ｘcos72°, Ｘsin72°，Ｘ）
　Ｋ：（-Ｘ，０，Ｘ）
　Ｍ：（-Ｘcos72°，-Ｘsin72°，Ｘ）
　Ｏ：（Ｘcos36°, -Ｘsin36°，Ｘ）

　Ｐ：（-１，０，Ｘ＋１）
　Ｑ：（-cos72°, -sin72°，Ｘ＋１）
　Ｒ：（cos36°, -sin36°，Ｘ＋１）
　Ｓ：（cos36°, sin36°，Ｘ＋１）
　Ｔ：（-cos72°, sin72°，Ｘ＋１）

次に、正１２面体を対角線（最も遠い点どうしを結んだ線）の方向から見たときの、
寸法を考えます。

上図のように、３つの正５角形が、平面の状態から、各辺が重なるまで傾けるとき、
正五角形の高さは、tan30°/tan36°に縮小されます。
また、下図において、対角線（例えばＡＰ）の長さｄは、
　
であり、高さ方向には、ｅ：ｆ＝ｆ：ｇ＝２：(√5+1) に分ければいいので、
　ｅ：ｆ：ｇ：ｆ：ｅ＝２：(√5+1）：（√5+3）：(√5+1）：２
となります。

以上より、上図の寸法を求めると、
　ａ＝√{(5+√5)/6}
　ｂ＝(1+cos36°)tan30°/tan36°
　ｃ＝sin36°
　
　ｅ＝2ｄ/(9+3√5)
　ｆ＝ｄ(√5+1)/(9+3√5)
　ｇ＝ｄ(√5+3)/(9+3√5)
となります。

「算数・数学」の部屋に戻る