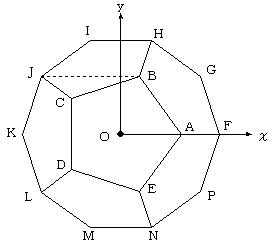
上図は、正12面体の1つの面をxy平面上に置いた図です。
正5角形ABCDEの外接円の中心を、原点Oとし、頂点Aをχ軸上に取ります。
A:(1,0,0)と置きます。(最終的には、AB=1 となるように倍率補正します)
このとき、B、Cの座標は
B:(cos72°,sin72°,0)、C:(-cos36°,sin36°,0)
となります。
また、ABの長さは、
AB=2sin36°
です。
一方、正5角形CDLKJは、正5角形ABCDEをCDを軸にして、回転した位置にあるので、
点Jのy座標は、点Bと同じです。
また、図形の対称性から、3点OCJは、同一平面上(上図では一直線上)にあります。
このことから、上図で、点Jは、点Cを sin72°/ sin36°倍した点になります。
Jのχ座標は、
-cos36°・sin72°/sin36°=-2cos236°
J:(-2cos236°,sin72°,z)とおいて、CJ=AB となるように、zの値を決めると、
(cos36°−2cos236°)2+(sin72°−sin36°)2+z2=4sin236°
これをz>0で解いて、z=1
これを用いて、各頂点のz座標を出すと、下図のようになります。
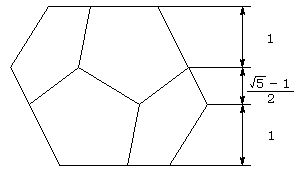
ここで、正12面体の中心(外接球の中心)と、各面までの距離は、
1+(√5−1)/4=(√5+3)/4
であることが分かります。
正12面体の体積は、1つの正5角形と、正12面体の中心とでできる5角錐の
12倍ですから、まず1つの5角錐の体積を求めます。
底面の正5角形の面積は、5/2×1×1×sin72°=5/2・√((5+√5)/8)
5角錐の体積は、1/3×5/2・√((5+√5)/8)×(√5+3)/4
これを12倍して、正12面体の体積は、5(√5+3)/2×√((5+√5)/8)
ただしこれは、1辺が、AB=2sin36°の場合なので、1辺が1に換算するため、
8sin336°で割って、整理すると、以下の体積を得ます。
体積=
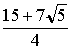
「算数・数学」の部屋に戻る