つまり 1≦t のとき
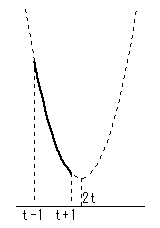
x=t-1 で最大
x=t+1 で最小
つまり 0<t<1
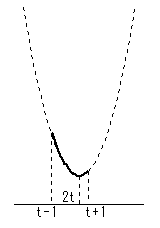
x=t-1 で最大
x=2t で最小
つまり t=0 のとき
x=t-1,t+1 で最大
x=2t で最小
つまり -1<t<0 のとき
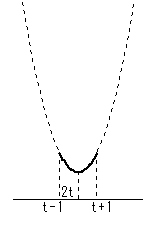
x=t+1 で最大
x=2t で最小
つまり t≦-1 のとき
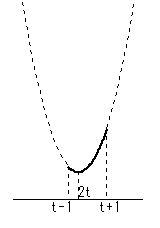
x=t+1 で最大
x=t-1 で最小
yukikoさんからの質問1
問題
f(x)=x2-4tx-2t+1
のt-1≦x≦t+1における最大値をM(t),最小値をm(t)とするとき、
次の各問いに答えよ。ただし,tは定数とする。
(1) M(t),m(t)をtを用いて表せ。
(2) M(t)-m(t)の最小値を求めよ。
解答
(1)
2次関数の最大最小の説明を元に、式を変形すると、
f(x)=(x-2t)2-4t2-2t+1
よって、f(x) は xが全実数をとるとき、 x=2t
で最小値 -4t2-2t+1 をとる。
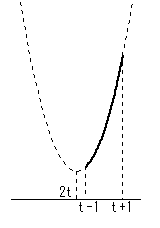
定義域 t-1≦x≦t+1 を考えるとき、最大、最小の位置は
定義域の両端 x=t-1、x=t+1、定義域の中央値
x=t、頂点のx座標 x=2t の
大小により次の5通りに分けられる。
| 1. t-1<t+1≦2t のとき つまり 1≦t のとき x=t-1 で最大 x=t+1 で最小 |
2.t-1<t<2t<t+1 のとき つまり 0<t<1 x=t-1 で最大 x=2t で最小 |
3. t-1<t=2t<t+1 のとき つまり t=0 のとき x=t-1,t+1 で最大 x=2t で最小 |
4.t-1<2t<t<t+1 のとき つまり -1<t<0 のとき x=t+1 で最大 x=2t で最小 |
5. 2t≦t-1<t+1 のとき つまり t≦-1 のとき x=t+1 で最大 x=t-1 で最小 |
 |
 |
 |
 |
 |
f(t-1)=-3t2+2、f(t+1)=-3t2-4t+2、f(2t)=-4t2-2t+1 であるから、
まとめると、
M(t)=-3t2-4t+2 (t≦0)
-3t2+2 (t>0)
m(t)=-3t2+2 (t≦-1)
-4t2-2t+1 (-1<t<1)
-3t2-4t+2 (1≦t)
(2) M(t), m(t) の値をまとめると以下のようになる。
| t | t≦-1 | -1<t≦0 | 0<t<1 | 1≦t |
| M(t) | -3t2-4t+2 | -3t2-4t+2 | -3t2+2 | -3t2+2 |
| m(t) | -3t2+2 | -4t2-2t+1 | -4t2-2t+1 | -3t2-4t+2 |
| M(t)-m(t) | -4t | t2-2t+1=(t-1)2 | t2+2t+1=(t+1)2 | 4t |
y=M(x)-m(x) のグラフは以下のようになる。
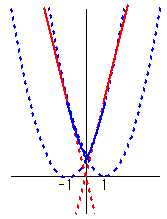
青は放物線、赤は直線である。
よって、M(t)-m(t) の最小値は t=0 のとき 1
算数・数学の部屋に戻る