2次関数の最小値・最大値について、まとめておきます。
2次関数
y=ax2+bx+c (a≠0)
は、変形すると
y=a(x2+bx/a)+c
y=a{x2+2×bx/2a+(b/2a)2 - (b/2a)2} +c
y=a(x+b/2a)2 - b2/4a+c
y=a(x+b/2a)2+(- b2+4ac)/4a
よって、
y=ax2+bx+c
のグラフは、
y=ax2
のグラフを、x軸方向に −b/2a、y軸方向に (- b2+4ac)/4a だけ
平行移動したグラフになります。
グラフの形はaの正負によって、2通りあります。
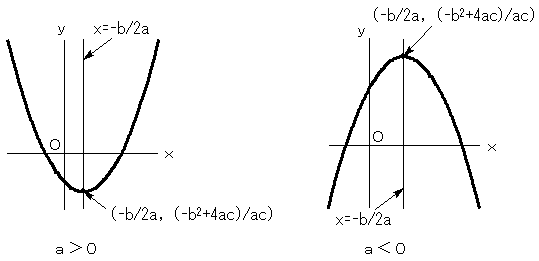
左のグラフを下に凸のグラフ、右のグラフを上に凸のグラフと言います。
また、グラフ上の点(-b/2a, (-b2+4ac)/4a ) を頂点、頂点を通りy軸に平行な
直線(x=-b/2a)を軸と言います。
xがすべての値を取るとき、
下に凸のグラフは、頂点で最小値となり、最大値はありません。
上に凸のグラフは、頂点で最大値となり、最小値はありません。
※頂点のy座標(-b2+4ac)/4a で、最大または最大になるということです。
問題によっては、xの値の範囲(定義域と言います)が限られていて、その範囲内での
最大・最小を求める場合があります。
下に凸のグラフを例に取ると、
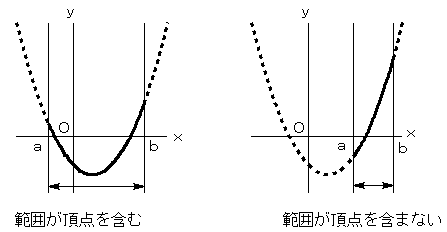
頂点が範囲内にあるときは、
頂点で最小値、範囲の両端の小さくない方が最大値
頂点が範囲内にないときは
範囲の両端の小さい方が最小値、大きい方が最大値
となります。
上に凸の場合は、この逆です。
「算数・数学」の部屋に戻る