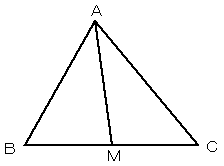
中線定理（これはパップスの定理とも言いますが、こちらとは別物です）
三角形ＡＢＣにおいて、辺ＢＣの中点をＭとするとき、
線分ＡＭを中線という。このとき、
　ＡＢ²＋ＡＣ²＝２(ＡＭ²＋ＢＭ²)
が成り立つ。

拡張形（これはスチュワートの定理と同じです）
三角形ＡＢＣで、辺ＢＣをｍ：ｎの比に内分する点をＰとするとき、
　ｎＡＢ²＋ｍＡＣ²＝ｎＢＰ²＋ｍＣＰ²＋（ｍ＋ｎ）ＡＰ²
が成り立つ


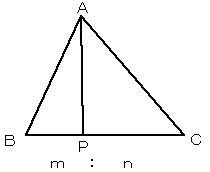
証明
拡張形で、ｍ＝ｎ≠０とおけば、元の中線定理に一致するので、拡張形の
証明のみ行う。

　△ＡＢＰ、△ＡＣＰにおいて、余弦定理より、
　　ＡＢ²＝ＡＰ²＋ＢＰ²−２ＡＰ・ＢＰcos∠ＡＰＢ・・・(1)
　　ＡＣ²＝ＡＰ²＋ＣＰ²−２ＡＰ・ＣＰcos∠ＡＰＣ・・・(2)
　ｎＢＰ＝ｍＣＰ　および　cos∠ＡＰＢ＝cos(180°−∠ＡＰＣ)＝−cos∠ＡＰＣ
　より、(1)×ｎ＋(2)×ｍ　を計算して、
　　ｎＡＢ²＋ｍＡＣ²＝ｎ(ＡＰ²＋ＢＰ²)＋ｍ(ＡＰ²＋ＣＰ²)
　整理して
　　ｎＡＢ²＋ｍＡＣ²＝ｎＢＰ²＋ｍＣＰ²＋（ｍ＋ｎ）ＡＰ²
　証明終わり

「算数・数学の部屋」に戻る