ACの傾きは−DCです。必ず一方が正、一方が負になります。
ABとACが直行しているので、
△ABDと△CADは相似となり、
AD:BD=DC:AD
となります。AD=1 であるので、
BD・DC=1
となります。一方、傾きどうしの積は、−BD・DC であり、
これは、−1になります。
ウツノミヤンさんからの質問
1,どうして直交する二直線の傾きの積は−1なのですか?
2,どうして数学的帰納法による証明は正しいといえるのでしょうか?n+100なら違っているかもしれないじゃないですかぁ……。
| n | n(n+1)(2n+1) | ||
| 3. | Σ | k2= | -------------- |
| k=1 | 6 |
の公式がどういう理屈で成り立っているのか分かりません。証明はできます。
| n | n-1 | ||
| Σ | k3 = 1+ | Σ | (k+1)3 |
| k=1 | k=1 |
を解けば出せますし、数学的帰納法でもスマートに出せます。
しかし、理解は出来ても納得出来ないのです。
これだと、Σk3の一般項を出そうとしてたまたま導き出せたような気がします。
「これはテクニックだ」なんて余計に納得出来ません。
Σk2の意味に沿った解説というものは出来ないのでしょうか。
4,不良の矢田まさる君が、どうして今回は魔女に格上げなのでしょうか?(笑)
5,丹下桜さんに声優復帰して欲しいと願うのは僕だけでしょうか?
回答
1. ここでは、当然、x軸やy軸に平行な直線は扱わず、その他の直線について考えます。
傾きとは、xが1増えたときにyがどれだけ変化するかという量です。
 |
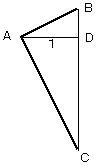
左図のように、直行する2直線AB、ACがあるとき、ABの傾きはBD ACの傾きは−DCです。必ず一方が正、一方が負になります。 ABとACが直行しているので、 △ABDと△CADは相似となり、 AD:BD=DC:AD となります。AD=1 であるので、 BD・DC=1 となります。一方、傾きどうしの積は、−BD・DC であり、 これは、−1になります。 |
2. 数学的帰納法の仕組みは、
ある規則的な数列An(nは自然数)(通常Anは自然数であることが多い)の任意の項について
成り立っていることを示したい命題があるとき、
(1) 数列の初項A1について命題が成り立つことを示す。
(2) 数列上の任意の連続する2項Ak,Ak+1において、Akについて命題が成り立つという条件下では、
Ak+1についても、命題が成り立つことを示す。
という論法です。ここで重要なのは、(2)
は数列上のどの連続する2項をとってもいいということです。
そして、A1について成り立つということが、既に示されていますので、A2についても成り立つ。
そうすると、A3についても成り立つ。よって、A4についても成り立つ。従って、A5についても成り立つ。
ゆえに...もういいね。
そして、このつながりは途中で切れることはありません。(2)
は特別に選んだ連続する2項について
成り立つのではなく、すべての連続する2項について、成り立つからです。
3. Σk2 の証明は、Σk のように、順番を入れ換えて一発というわけには行きません。
1から100までの自然数の和参照。
Σk3 からの副産物のようなものはイヤといわれるなら、こんなのはどうでしょう?
やはり、多少テクニック(式のいじくり)を使いますが。
12= 1
22= 1 + 3
32= 1 + 3 + 5
52= 1 + 3 + 5 + 7
・・・・・・
n2= 1 + 3 + 5 + 7 + ・・・ + (2n-1)
| n | n | ||
| Σ | k2=n・1+(n-1)・3+(n-2)・5+・・・+(n-k+1)(2k-1)+・・・1・(2n-1)= | Σ | (n-k+1)(2k-1) |
| k=1 | k=1 |
(以下Σの範囲省略)
Σk2=Σ{-2k2+(2n+3)k-(n+1)}
3Σk2=Σ{(2n+3)k-(n+1)}=(2n+3)n(n+1)/2-n(n+1)
=n(n+1)(2n+1)/2
よって、
Σk2=n(n+1)(2n+1)/6