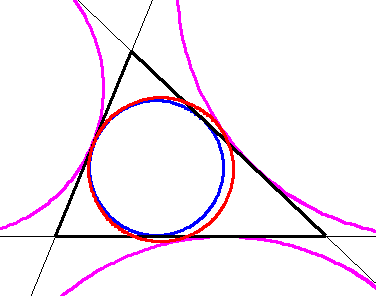
フォイエルバッハ(Feuerbach)の定理

三角形において その九点円は 内接円に内接し 傍接円に外接する。
関連定理：九点円の定理



証明
内接円と接することの証明
ＡＢ＝ＡＣのときは、明らかに、ＢＣの中点で、接するので、ＡＢ＞ＡＣとします。

内接円に接する証明
図１ ＢＣ，ＣＡ，ＡＢの中点をそれぞれＤ，Ｅ，Ｆとし、ＡからＢＣに下ろした垂線の足をＧ、∠ＢＡＣの二等分線とＢＣとの交点をＪ、ＣをＡＪに対して対称に移動した点（ＡＢ上にある）をＨ、ＡＪとＣＨの交点をＫとします。
また、内接円と、ＢＣ，ＣＡ，ＡＢとの接点をそれぞれＸ，Ｙ，Ｚとします。
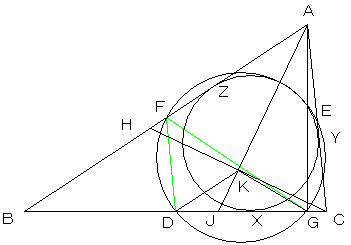図１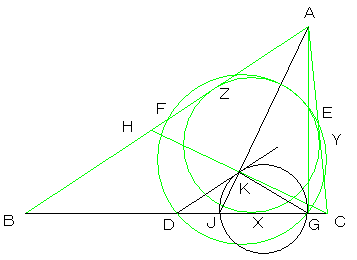

図２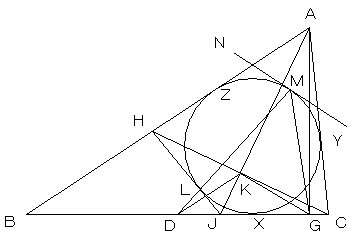
図３
弦ＤＧに立つ九点円の円周角（∠ＤＦＧで代表）は、
　∠ＡＣＢ−∠ＡＢＣ
となります。なぜなら、三角形の外角の性質より
　∠ＤＦＧ＝∠ＦＤＢ−∠ＦＧＤ
これにおいて、ＦＤ//ＡＣ（中点連結定理より）より、
　∠ＦＤＢ＝∠ＡＣＢ
また、ＧＦは、直角三角形ＡＧＢの直角と斜辺の中点を
結んだ線なので、ＦＧ＝ＦＢ であり、△ＢＦＧは二等辺三角形となり、
　∠ＦＧＤ＝∠ＡＢＣ
以上より、
　∠ＤＦＧ＝∠ＡＣＢ−∠ＡＢＣ　・・・・・・（１）
ＤはＢＣの中点ですので、
　ＤＸ＝(ＢＸ−ＸＣ)/２
　　　＝(ＢＺ−ＣＹ)/２
　　　＝{(ＢＺ＋ＺＡ)−(ＣＹ＋ＹＡ)}/２
　　　＝(ＡＢ−ＡＣ)/２　・・・・・・（２）
△ＡＣＨはＡＣ＝ＡＨの二等辺三角形であり、ＫはＣＨの中点であるので、△ＢＨＣと△ＤＫＣにおいて、中点連結定理より、
　ＤＫ＝ＢＨ/２＝(ＡＢ−ＡＨ)/２
　　　＝(ＡＢ−ＡＣ)/２
（２）　より、
　ＤＸ＝ＤＫ　・・・・・・（３）
また、ＤＫ//ＢＨ　より
　∠ＤＫＪ＝∠ＢＡＪ　・・・・・・（４）
∠ＡＫＣ＝∠ＡＧＣ＝90°　より、４点Ａ，Ｋ，Ｇ，Ｃは、同一円上にある。つまり、四角形ＡＫＧＣにおいて、
　∠ＫＡＣ＋∠ＫＧＣ＝180°
よって、
　∠ＫＧＤ＝∠ＫＡＣ　・・・・・・（５）
（４）（５）および、ＡＪが∠ＢＡＣの二等分線であることより、
　∠ＤＫＪ（＝∠ＢＡＪ＝∠ＫＡＣ）＝∠ＫＧＤ　・・・・・・（６）
図２ よって、接弦定理の逆より、３点Ｋ，Ｊ，Ｇを通る円を描けば、ＤＫは、その円の接線となります。
方べきの定理より
　ＤＫ2＝ＤＪ・ＤＧ
（３）より、
　ＤＸ2＝ＤＪ・ＤＧ　・・・・・・（７）
図３ △ＡＪＣと△ＡＪＨの対称性より、ＪＨは△ＡＢＣの内接円に接しその接点をＬとします。
ＤＬの延長線とこの内接円の交点（Ｌでない方の点）をＭとすると、方べきの定理より
　ＤＸ2＝ＤＬ・ＤＭ
（７）より、
　ＤＬ・ＤＭ＝ＤＪ・ＤＧ
方べきの定理の逆より、４点Ｌ，Ｊ，Ｇ，Ｍは、同一円上にあります。よって、四角形ＬＪＧＭにおいて、
　∠ＤＪＬ＝∠ＬＭＧ　・・・・・・（８）
　∠ＨＬＭ＝∠ＪＧＭ　・・・・・・（９）　
△ＢＨＪにおける外角の定理より、
　∠ＤＪＬ＝∠ＡＨＪ−∠ＡＢＣ＝∠ＡＣＢ−∠ＡＢＣ
（１）（８）より、
　∠ＤＭＧ＝∠ＤＦＧ
よって、点Ｍは、九点円上にあります。
次に九点円と内接円が点Ｍで接することを証明します。
点Ｍにおいて、内接円の接線ＭＮを引くと、弦ＬＭの両端に接線を引いたことになり、
　∠ＮＭＬ＝∠ＨＬＭ
（９）より、
　∠ＮＭＤ＝∠ＤＧＭ
∠ＤＧＭは、ＤＭを弦として九点円上に立つ円周角であり、これが∠ＮＭＤに等しいので、接弦定理の逆より、ＮＭは九点円の接線と分かります。
以上より、内接円と九点円は、共に点Ｍにおいて、直線ＮＭに接するので、この２円は接することが分かります。

傍接円に接する証明
図１ ＢＣ，ＣＡ，ＡＢの中点をそれぞれＤ，Ｅ，Ｆとし、ＡからＢＣに下ろした垂線の足をＧ、∠ＢＡＣの二等分線とＢＣとの交点をＪ、ＣをＡＪに対して対称に移動した点（ＡＢ上にある）をＨ、ＡＪとＣＨの交点をＫとします。
また、頂点Ａに対応する傍接円と、ＢＣ，ＣＡ，ＡＢとの接点をそれぞれＸ，Ｙ，Ｚとします。
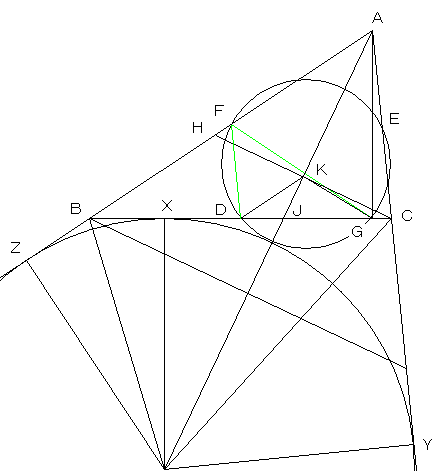図１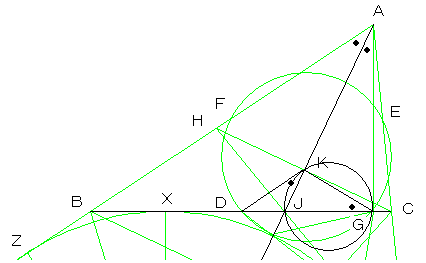

図２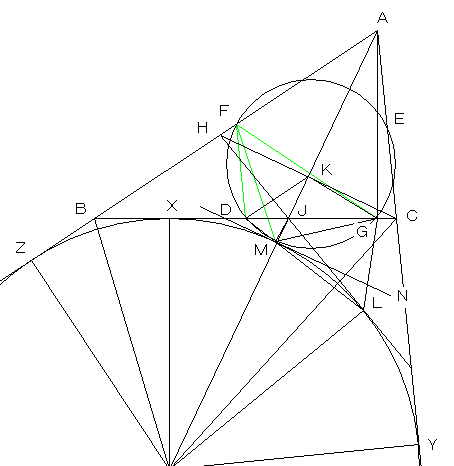

図３
弦ＤＧに立つ九点円の円周角（∠ＤＦＧで代表）は、
　∠ＡＣＢ−∠ＡＢＣ
となります。なぜなら、三角形の外角の性質より
　∠ＤＦＧ＝∠ＦＤＢ−∠ＦＧＤ
これにおいて、ＦＤ//ＡＣ（中点連結定理より）より、
　∠ＦＤＢ＝∠ＡＣＢ
また、ＧＦは、直角三角形ＡＧＢの直角と斜辺の中点を
結んだ線なので、ＦＧ＝ＦＢ であり、△ＢＦＧは二等辺三角形となり、
　∠ＦＧＤ＝∠ＡＢＣ
以上より、
　∠ＤＦＧ＝∠ＡＣＢ−∠ＡＢＣ　・・・・・・（１）
ＤはＢＣの中点ですので、
　ＤＸ＝(ＣＸ−ＸＢ)/２
　　　＝(ＣＹ−ＢＺ)/２
　　　＝{(ＡＹ−ＡＣ)−(ＡＺ−ＡＢ)}/２
　　　＝(ＡＢ−ＡＣ)/２　・・・・・・（２）
△ＡＣＨはＡＣ＝ＡＨの二等辺三角形であり、ＫはＣＨの中点であるので、△ＢＨＣと△ＤＫＣにおいて、中点連結定理より、
　ＤＫ＝ＢＨ/２＝(ＡＢ−ＡＨ)/２
　　　＝(ＡＢ−ＡＣ)/２
（２）　より、
　ＤＸ＝ＤＫ　・・・・・・（３）
また、ＤＫ//ＢＨ　より
　∠ＤＫＪ＝∠ＢＡＪ　・・・・・・（４）
∠ＡＫＣ＝∠ＡＧＣ＝90°　より、４点Ａ，Ｋ，Ｇ，Ｃは、同一円上にある。つまり、四角形ＡＫＧＣにおいて、
　∠ＫＡＣ＋∠ＫＧＣ＝180°
よって、
　∠ＫＧＤ＝∠ＫＡＣ　・・・・・・（５）
（４）（５）および、ＡＪが∠ＢＡＣの二等分線であることより、
　∠ＤＫＪ（＝∠ＢＡＪ＝∠ＫＡＣ）＝∠ＫＧＤ　・・・・・・（６）
図２ よって、接弦定理の逆より、３点Ｋ，Ｊ，Ｇを通る円を描けば、ＤＫは、その円の接線となります。
方べきの定理より
　ＤＫ2＝ＤＪ・ＤＧ
（３）より、
　ＤＸ2＝ＤＪ・ＤＧ　・・・・・・（７）
図３ △ＡＪＣと△ＡＪＨの対称性より、ＪＨは△ＡＢＣの傍接円に接しその接点をＬとします。
ＤＬの延長線とこの傍接円の交点（Ｌでない方の点）をＭとすると、方べきの定理より
　ＤＸ2＝ＤＬ・ＤＭ
（７）より、
　ＤＬ・ＤＭ＝ＤＪ・ＤＧ
方べきの定理の逆より、４点Ｌ，Ｇ，Ｊ，Ｍは、同一円上にあります。よって、四角形ＬＧＪＭにおいて、
　∠ＨＪＢ＝∠ＧＪＬ＝∠ＬＭＧ　・・・・・・（８）
△ＢＨＪにおける外角の定理より、
　∠ＨＪＢ＝∠ＡＨＪ−∠ＡＢＣ＝∠ＡＣＢ−∠ＡＢＣ
（１）（８）より、
　∠ＬＭＧ＝∠ＤＦＧ
　∠ＤＭＧ＋∠ＤＦＧ＝180°
よって、四角形ＤＦＧＭは、九点円に内接し、点Ｍは、九点円上にあります。
次に九点円と傍接円が点Ｍで接することを証明します。
点Ｍにおいて、傍接円の接線ＭＮを引くと、弦ＬＭの両端に接線を引いたことになり、
　∠ＮＭＬ＝∠ＨＬＭ
また、円周角より、
　(∠ＮＭＬ＝)∠ＨＬＭ＝∠ＭＧＤ＝∠ＭＦＤ　・・・・・・（９）
（１）（８）（９）より、
　∠ＮＭＧ＝∠ＬＭＧ−∠ＮＭＬ
　　＝∠ＤＦＧ−∠ＭＦＤ＝∠ＭＦＧ
∠ＭＦＧは、ＭＧを弦として九点円上に立つ円周角であり、これが∠ＮＭＧに等しいので、接弦定理の逆より、ＮＭは九点円の接線と分かります。
以上より、傍接円と九点円は、共に点Ｍにおいて、直線ＮＭに接するので、この２円は接することが分かります。

「算数・数学の部屋」に戻る